.Problema para ajudar na escola: Cálculos em uma pescaria

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)

---

André foi pescar com seu pai.
Na hora do lanche, ele sentou embaixo de uma árvore e, observando uma casa na margem oposta do rio, ficou curioso em saber qual seria a distância entre ela e a árvore sob a qual ele estava lanchando. Pensou, pensou e bolou uma maneira de calcular a distância.
Observe, na figura abaixo, o procedimento que André utilizou para descobrir a distância entre a árvore [tex]A[/tex] e a casa [tex]C[/tex].

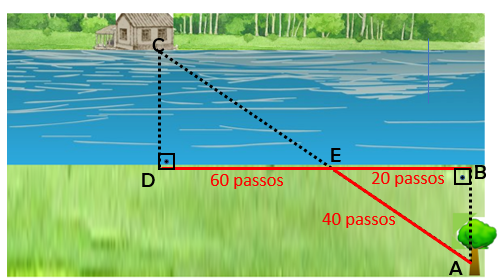
Sabendo que a medida do passo de André é [tex]70 \, [/tex]cm, determine a distância entre a casa e a árvore.
(Na figura, considere que os pontos [tex]A \, , \, E \, , \, C[/tex] são colineares, assim como [tex]D \, , \, E \, ,B \, .[/tex])

Solução

---

Observando os triângulos [tex]ABE[/tex] e [tex]CDE[/tex] notamos que:

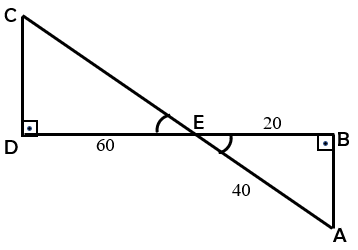
• os ângulos [tex]A\hat{E}B[/tex] e [tex]C\hat{E}D[/tex] são congruentes, pois são opostos pelo vértice;
• os ângulos [tex]A\hat{B}E[/tex] e [tex]C\hat{D}E[/tex] são congruentes, pois ambos são ângulos retos.

Logo, pelo Lembrete (2), concluímos que os triângulos [tex]ABE[/tex] e [tex]CDE[/tex] são semelhantes e, dessa forma, os lados correspondentes desses dois triângulos são proporcionais. Em particular, se o comprimento do segmento [tex]\overline{CE}[/tex] é [tex]x[/tex] passos, segue que
[tex]\qquad \dfrac{60}{20}=\dfrac{x}{40}[/tex]
[tex]\qquad \\
\qquad x=\dfrac{60\times 40}{20}\\
\, \, [/tex]
[tex]\qquad x=120[/tex] passos
e, assim, a distância entre a árvore [tex]A[/tex] e a casa [tex]C[/tex] é de [tex]120+40=160[/tex] passos.
Mas cada passo de André equivale a [tex]70 \, [/tex]cm; portanto, a distância entre a árvore e a casa é [tex]160 \times 70=11 \, 200 \, [/tex]cm ou, ainda, [tex] \, \fcolorbox{black}{#eee0e5}{$ \text{112 metros}$} \, .[/tex]

---

Solução elaborada pelos Moderadores do Blog.