Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
As arestas de um cubo são numeradas de 1 a 12.
Em seguida, associamos a cada vértice desse cubo a soma dos números atribuídos às arestas que incidem neste vértice. (Veja duas ilustrações dessas associações na figura abaixo.)
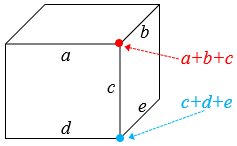
Os valores associados aos vértices podem ser todos iguais?
Extraído da OBM Sênior, 1994.
Solução
Vamos supor que os valores associados aos vértices do cubo sejam todos iguais a [tex]x[/tex]. Perceba que [tex]x[/tex] é um número natural, já que é soma de números naturais de [tex]1[/tex] a [tex]12\,.[/tex]
Como o cubo tem oito vértices e cada aresta incide em dois vértices distintos, ao somarmos os oito valores associados aos vértices segue que:
[tex] \qquad 8x=2 \cdot \left(1+2+3+4+5+6+7+8+9+10+11+12\right)[/tex]
[tex] \qquad \cancel{8}x=\cancel{2} \cdot 78[/tex]
[tex] \qquad \cancel{4}x=\cancel{78}[/tex]
[tex] \qquad \boxed{2x=39}\,[/tex].
Mas, como [tex]x \in \mathbb{N}[/tex], a igualdade [tex]2x=39[/tex] nos garante que [tex]39[/tex] é um número par, o que é um absurdo!
Com isso, concluímos que os valores associados aos vértices NÃO podem ser todos iguais.
 |
Se você ficou em dúvida com relação à afirmação de que "cada aresta incide em dois vértices distintos", utilize o applet abaixo. |
Um applet para ajudar
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para ver a soma dos números de arestas que incidem em cada vértice, clique no quadradinho correspondente ao vértice que aparece na parte inferior do aplicativo.
(3) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
