✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
As retas [tex]r[/tex] e [tex]s[/tex] são paralelas.
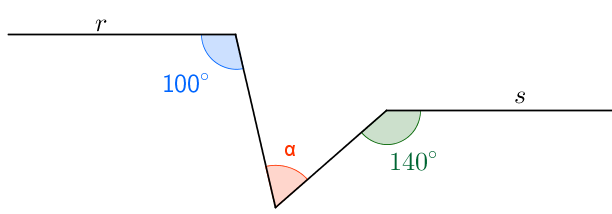
Qual a medida angular [tex]\alpha[/tex] ?

Ajuda
Quando duas retas distintas [tex]r \, [/tex] e [tex] \, s[/tex], paralelas ou não, são intersectadas por uma transversal, automaticamente fica definida uma família de oito ângulos. Particularmente, quando [tex]r \, [/tex] e [tex] \, s[/tex] forem paralelas, alguns ângulos da família têm a mesma medida.
Se você não se lembra disso, clique AQUI antes de resolver este problema.
Solução 1
A reta [tex]k[/tex] é uma das retas que definem o ângulo cuja medida [tex]\alpha[/tex] iremos determinar, conforme mostra a figura abaixo.
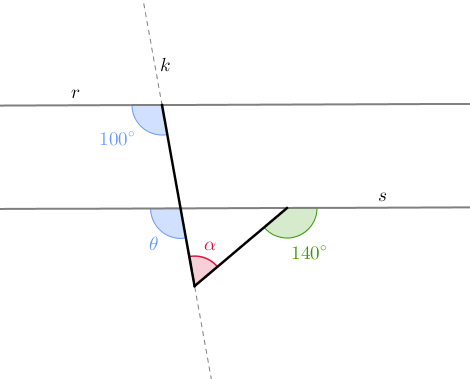
Como os ângulos que aparecem na figura com medidas [tex]\textcolor{#6699FF}{\theta}[/tex] e [tex]\textcolor{#6699FF}{100^\circ}[/tex] são "ângulos correspondentes" definidos pelas retas paralelas [tex]r \, [/tex] e [tex] \, s \, [/tex] e a transversal [tex]k[/tex], então [tex]\textcolor{#6699FF}{\theta=100^\circ}[/tex].
Com isso, [tex]\textcolor{#DC143C}{\alpha} \, [/tex] é a medida de um dos ângulos internos de um triângulo cujas medidas dos outros dois ângulos internos são [tex]80^\circ[/tex] e [tex]40^\circ[/tex].
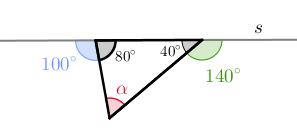
Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], então [tex]\boxed{40^\circ+80^\circ+\textcolor{#DC143C}{\alpha}=180^\circ}[/tex], donde [tex]\fcolorbox{black}{#F6A2B0}{$\alpha= 60^\circ $}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sejam [tex]t \, [/tex] e [tex] \, k[/tex] as retas que definem o ângulo cuja medida [tex]\alpha[/tex] iremos determinar.
Pelo vértice desse mesmo ângulo trace a reta [tex]w[/tex], paralela às retas [tex]r \, [/tex] e [tex] \, s[/tex] definidas no problema.
Observe na figura abaixo que ficamos, então, com três retas paralelas [tex]r[/tex], [tex]s \, [/tex] e [tex] \, w[/tex], intersectadas pelas transversais [tex]t \, [/tex] e [tex] \, k[/tex].
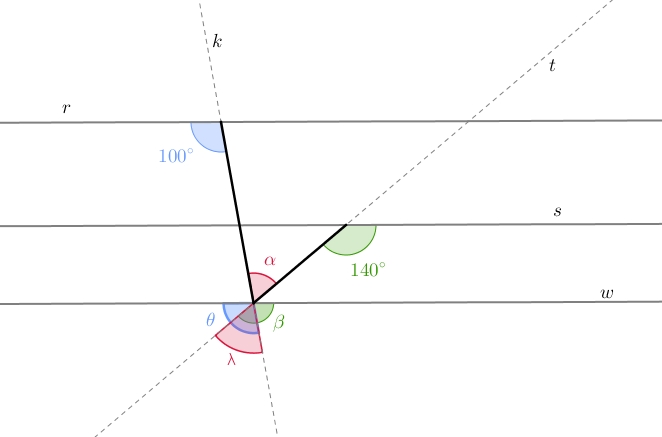
Perceba que os ângulos de medidas angulares [tex]\textcolor{#DC143C}{\alpha} \, [/tex] e [tex] \, \textcolor{#DC143C}{\lambda}[/tex] são opostos pelo vértice (OPV), logo [tex]\textcolor{#DC143C}{\alpha=\lambda} \, [/tex] e, dessa forma, vamos determinar [tex] \, \textcolor{#DC143C}{\lambda}[/tex].
Perceba que:
- Os ângulos que aparecem na figura e cujas medidas são [tex]\textcolor{#6699FF}{\theta}[/tex] e [tex]\textcolor{#6699FF}{100^\circ}[/tex] são ângulos correspondentes definidos pelas retas paralelas [tex]r \, [/tex] e [tex]w \, [/tex] e a transversal [tex]k[/tex]; logo, [tex]\textcolor{#6699FF}{\theta=100^\circ}[/tex];
- Os ângulos que aparecem na figura e cujas medidas são [tex]\textcolor{#339900}{\beta}[/tex] e [tex]\textcolor{#339900}{140^\circ}[/tex] são ângulos correspondentes definidos pelas retas paralelas [tex]s \, [/tex] e [tex]w \, [/tex] e a transversal [tex]t[/tex]; logo, [tex]\textcolor{#339900}{\beta=140^\circ}[/tex].
Como [tex]\textcolor{#6699FF}{\theta}-\textcolor{#DC143C}{\lambda}+\textcolor{#339900}{\beta}=180^\circ[/tex], segue que:
[tex]\qquad \textcolor{#DC143C}{\lambda}=\textcolor{#6699FF}{\theta}+\textcolor{#339900}{\beta}+180^\circ[/tex]
[tex]\qquad \textcolor{#DC143C}{\lambda}=\textcolor{#6699FF}{100^\circ}+\textcolor{#339900}{140^\circ}+180^\circ[/tex]
[tex]\qquad \textcolor{#DC143C}{\lambda}=\textcolor{#DC143C}{60^\circ}[/tex]
e, assim, [tex]\fcolorbox{black}{#F6A2B0}{$\alpha= 60^\circ$}[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
