✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil )
Um cubo com arestas de um metro cada está encostado em um muro vertical.
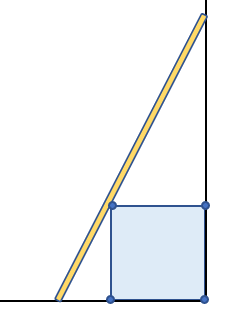
Uma escada de comprimento [tex]\sqrt{15}[/tex] metros está apoiada no muro e toca a aresta livre do cubo, conforme indica a vista lateral da escada tocando o piso, o cubo e a parede, mostrada na figura abaixo.
Qual a altura máxima, com relação ao piso, que o extremo superior da escada pode alcançar?
Solução
Vamos supor que o extremo superior da escada esteja a uma altura de [tex]h[/tex] metros e que a distância do pé da escada até a parede seja [tex]d[/tex] metros.
Assim, utilizando o Teorema de Pitágoras, obtemos uma primeira equação:
[tex]\qquad \, \fcolorbox{black}{#d7d7d7}{$h^2+d^2=\left(\sqrt{15}\right)^2=15$}\, . \qquad \textcolor{#800000}{(i)}[/tex]
Essa equação registra uma posição fixa da escada; vamos, então buscar uma equação que envolva os deslocamentos da escada. Para isso, vamos supor que o extremo superior da escada esteja a uma distância de [tex]x[/tex] metros do cubo e que a distância do pé da escada ao cubo seja [tex]z[/tex] metros, de acordo com a figura abaixo.
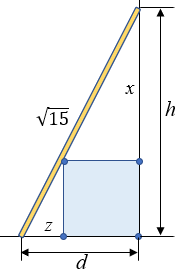
Assim:
[tex]\qquad h=x+1 \qquad \textcolor{#800000}{(ii)}[/tex]
[tex]\qquad d=z+1. \qquad \textcolor{#800000}{(iii)}[/tex]
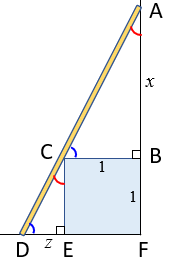
Por outro lado, [tex]BCEF[/tex] é a vista lateral do cubo no qual a escada está encostada, então [tex]BCEF[/tex] é um quadrado de lado [tex]1[/tex] metro.
Observe também que os segmentos [tex]\overline{CB}\, [/tex] e [tex]\, \overline{DF}[/tex] são paralelos, logo os triângulos [tex]ABC\, [/tex] e [tex]\, CED[/tex] são semelhantes e fornecem a seguinte proporção entre os lados correspondentes:
[tex]\qquad \dfrac{x}{1}=\dfrac{1}{z}[/tex],
donde
[tex]\qquad xz=1. \qquad \textcolor{#800000}{(iv)}[/tex]
Fazendo a multiplicação das equações [tex]\textcolor{#800000}{(ii)}\, [/tex] e [tex]\, \textcolor{#800000}{(iii)}[/tex] temos que:
[tex]\qquad hd=xz+x+z+1. \qquad \textcolor{#800000}{(v)}[/tex]
Substituindo [tex]\textcolor{#800000}{(iv)}\, [/tex] em [tex]\textcolor{#800000}{(v)}\, [/tex] e utilizando mais uma vez as igualdades [tex]\textcolor{#800000}{(ii)}\, [/tex] e [tex]\, \textcolor{#800000}{(iii)}[/tex], obtemos uma equação fundamental para a solução do problema:
[tex]\qquad hd=1+x+z+1[/tex]
[tex]\qquad hd=\underbrace{(x+1)}_{h}+\underbrace{(z+1)}_{d}[/tex]
[tex]\qquad \, \fcolorbox{black}{#d7d7d7}{$ hd=h+d$}. \qquad \textcolor{#800000}{(vi)}[/tex]
Como não temos mais informações geométricas relevantes, vamos atacar algebricamente o problema.
Elevando ao quadrado ambos os lados da igualdade [tex]\textcolor{#800000}{(vi)}\, [/tex] e, em seguida, utilizando a igualdade [tex]\textcolor{#800000}{(i)}\, [/tex], vemos que:
[tex]\qquad \left(hd\right)^2=\left(h+d\right)^2[/tex]
[tex]\qquad \left(hd\right)^2=\left(h^2+d^2\right)+2hd[/tex]
[tex]\qquad \left(hd\right)^2\stackrel{\textcolor{#800000}{(i)}}{=}15+2hd[/tex]
[tex]\qquad \left(hd\right)^2-2\left(hd \right)-15=0. \qquad \textcolor{#800000}{(vii)}[/tex]
Se fizermos [tex]y=hd[/tex] em [tex]\textcolor{#800000}{(vii)}\, [/tex], obtemos a equação do segundo grau [tex]y^2-2y-15=0[/tex], cujas raízes são:
[tex]\qquad y=\dfrac{2 \pm \sqrt{4+60}}{2}=\dfrac{2 \pm 8}{2}[/tex]
[tex]\qquad y_1=5\qquad [/tex] e [tex]\qquad y_2=-3. [/tex]
Como [tex]y=hd\, [/tex] e [tex]h[/tex] e [tex]d[/tex] representam comprimentos, concluímos que [tex]\boxed{y=hd=5}.[/tex]
Substituindo essa igualdade em [tex]\textcolor{#800000}{(vi)}\, [/tex], resulta que:
[tex]\qquad hd=h+d[/tex]
[tex]\qquad 5=h+\dfrac{5}{h}[/tex]
[tex]\qquad 5h=h^2+5[/tex]
[tex]\qquad \boxed{h^2-5h+5=0}\, .[/tex]
Temos mais uma equação do segundo grau, só que, desta feita, as raízes dessa equação fornecem posições do extremo superior da escada, com relação ao piso onde ela está apoiada. As raízes dessa equação são:
[tex]\qquad h=\dfrac{5 \pm \sqrt{25-20}}{2}=\dfrac{5 \pm \sqrt{5}}{2}\\\, [/tex]
[tex]\\
\qquad h_1=\dfrac{5 +\sqrt{5}}{2}\qquad [/tex] e [tex]\qquad h_2=\dfrac{5 -\sqrt{5}}{2}.[/tex]
Tanto [tex]h_1[/tex] como [tex]h_2[/tex] são números positivos, assim representam alturas a que está o extremo superior da escada. No entanto, queremos a maior altura [tex]h[/tex], portanto a resposta do problema é [tex]h=\dfrac{5 +\sqrt{5}}{2} [/tex], ou seja, a altura máxima, com relação ao piso, que o extremo superior da escada pode alcançar é aproximadamente [tex]\, \fcolorbox{black}{#eee0e5}{$3,6\, metros$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
