Problema
Considere um triângulo [tex]ABC[/tex].
Sobre o lado [tex]\overline{AC}[/tex], tome o ponto [tex]P[/tex] de modo que a soma das medidas dos lados [tex]\overline{BC}[/tex] e [tex]\overline{PC}[/tex] seja igual à medida do lado [tex]\overline{PA}[/tex], isto é, [tex]a+x=y.[/tex]
Seja [tex]M[/tex] o ponto médio do lado [tex]\overline{AB}[/tex].
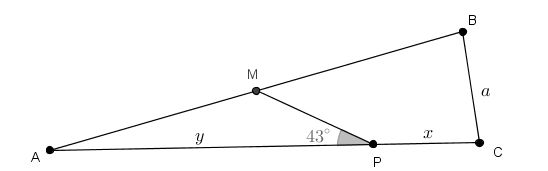
Se a medida do ângulo [tex]APM[/tex] é [tex]43^{\circ}[/tex], então a medida [tex]\theta[/tex], em graus, do ângulo [tex]ACB[/tex] é tal que:
- [tex]~40^{\circ}<\theta<50^{\circ}[/tex];
- [tex]~50^{\circ}<\theta<60^{\circ}[/tex];
- [tex]~60^{\circ}<\theta<70^{\circ}[/tex];
- [tex]~70^{\circ}<\theta<80^{\circ}[/tex];
- [tex]~80^{\circ}<\theta<90^{\circ}[/tex].
Solução
A princípio, vamos prolongar o segmento [tex]\overline{AC}[/tex] até o ponto [tex]D[/tex], de tal maneira que [tex]CD=a[/tex], como ilustrado na figura abaixo.
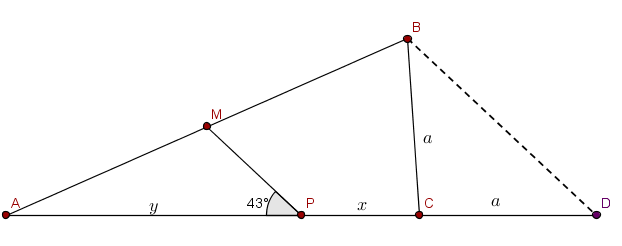
Sabemos que [tex]y=x+a[/tex], consequentemente [tex]PD=PC+CD= x + a = y = AP[/tex]. Logo [tex]P[/tex] é o ponto médio do segmento [tex]\overline{AD}[/tex].
Assim, [tex]\overline{PM}[/tex] é a base média do triângulo [tex]\triangle{ABD}[/tex](*), o que implica na semelhança [tex]\triangle{AMP} \cong \triangle{ABD}[/tex]. Com isso, [tex]\measuredangle BDC=\measuredangle{MPA} = 43^{\circ}[/tex].
Por outro lado [tex]BC=CD[/tex], assim o triângulo [tex]\triangle{BCD}[/tex] é isósceles de base [tex]\overline{BD}[/tex] e, portanto, [tex]\measuredangle{CBD} = \measuredangle{BDC} = 43^{\circ}[/tex].
Visto que a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex](**), concluímos que
[tex]\qquad \measuredangle{BCD} = 180^{\circ} – 2 \cdot 43^{\circ} =94^{\circ}[/tex].
Finalmente, segue que
[tex]\qquad \theta=\measuredangle{ACB} = 180^{\circ} – 94^{\circ} = 86^{\circ}[/tex].
Como [tex]80^{\circ} < 86^{\circ} < 90^{\circ}[/tex], a alternativa correta é a E.
(*) Se você não sabe o que é uma base média de um triângulo, clique AQUI.
(**) Visite a nossa Sala de Estudos Soma dos ângulos internos de um triângulo.
Solução elaborada pelo aluno do PIC-OBMEP Angelo Donizeti Lorenconi Junior.
