Problema
Devemos pintar os nove quadradinhos do tabuleiro [tex]3\times3[/tex] da figura, de modo que em cada linha, em cada coluna e em cada uma das duas diagonais não existam quadradinhos pintados com uma mesma cor.
Qual é o número mínimo de cores necessárias para que façamos a pintura?
Solução
Veja que nas diagonais do tabuleiro precisamos de três cores distintas para uma e duas cores distintas para outra.
Sendo 1, 2, 3, 4 e 5 as cores distintas, veja um exemplo:
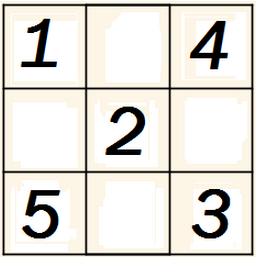O restante do tabuleiro pode ser pintado a partir dessas mesmas cores.Dessa forma, vemos que o número mínimo de cores é cinco.
Veja a seguir um exemplo de que isso é possível!
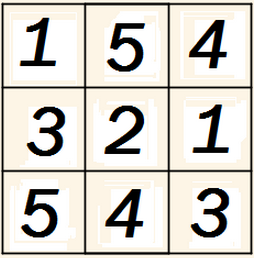
É importante observar que:
- Duas cores são insuficientes para pintarmos, sem repetições, qualquer linha, qualquer coluna ou qualquer diagonal.
- Utilizando apenas três cores distintas e respeitando as regras do problema, conseguiríamos pintar, por exemplo, uma diagonal. No entanto, precisaríamos de uma quarta cor para continuar; pois, do contrário, descumpriríamos as regras ao tentar pintar a última coluna, por exemplo.
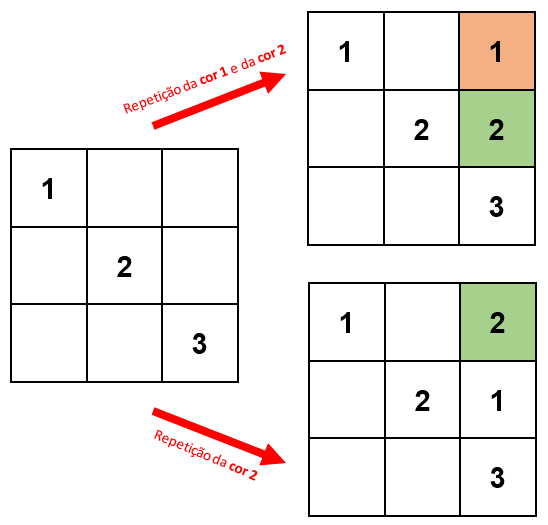
- Se utilizarmos uma quarta cor, também não conseguiremos finalizar a pintura, de acordo com as regras definidas. Teremos problemas para pintar, por exemplo, a outra diagonal, utilizando apenas as quatro cores.
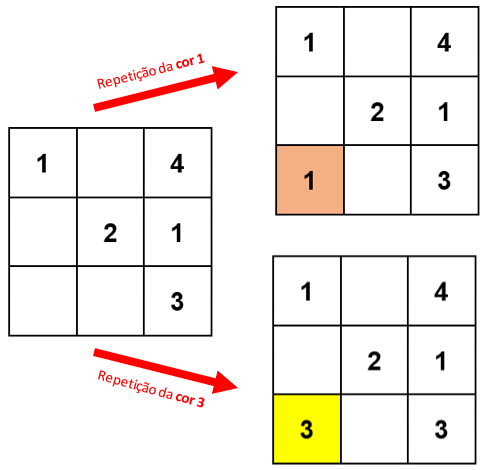
Dessa forma, o número mínimo de cores necessárias para que façamos a pintura é, de fato, cinco.
Solução elaborada pelo aluno do PIC-OBMEP Gil Vitor Bahr Yau, com contribuições dos Moderadores do Blog.