Problema
A um dado número natural [tex]a[/tex] somamos os dois números pares imediatamente posteriores a ele e os três números ímpares imediatamente anteriores a ele. A soma final é [tex]682[/tex].
Qual é a soma dos algarismos do número [tex]a[/tex]?
Solução
Chamemos os dois pares posteriores a [tex]a[/tex] de [tex]P_1[/tex] e [tex]P_2[/tex] e os três ímpares anteriores, de [tex]I_1,I_2[/tex] e [tex]I_3[/tex].
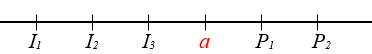
Sabemos que [tex](P_1+P_2)+a +(I_1+I_2+I_3)=682[/tex]; mas observamos que [tex](P_1+P_2)+(I_1+I_2+I_3)[/tex] é um número ímpar*, digamos [tex]I[/tex]. Assim [tex]a+I=682[/tex], donde concluímos que [tex]a[/tex] é um número ímpar*, já que a soma de um número par com um ímpar seria ímpar* e
Dessa forma, os pares posteriores ao número [tex]\,a\,[/tex] são [tex]\,a+1 \,[/tex] e [tex]\, a+3\, [/tex], enquanto os ímpares anteriores a [tex]\, a\,[/tex] são [tex]\, a-2\, [/tex], [tex]\, a-4\, [/tex] e [tex]\, a-6[/tex].
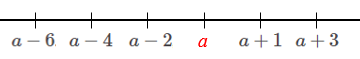
Com isso
[tex]\qquad a+(a+1)+(a+3)+(a-2)+(a-4)+(a-6)=682[/tex],
donde
[tex]\qquad 6a-8=682\\\qquad a = \dfrac{690}{6}[/tex]
e, portanto,
[tex]\qquad a=115[/tex].
Consequentemente, a soma dos algarismos de [tex]a[/tex] é [tex]1+1+5=\boxed{\,7\,}[/tex].
(*)Participe da discussão sobre paridades neste tópico das nossas Salas de Estudo.
Solução elaborada pelo aluno do PIC-OBMEP Adrian Alexander Ticona Delgado, com contribuições dos Moderadores do Blog.
