Problema
(Indicado a partir do 9º ano do E. F.)
Há registros de que os agrimensores do Egito Antigo utilizavam uma corda dividida em 12 partes iguais por 11 nós para construírem triângulos com lados medindo 3, 4 e 5 e, com isso, demarcarem ângulos retos.
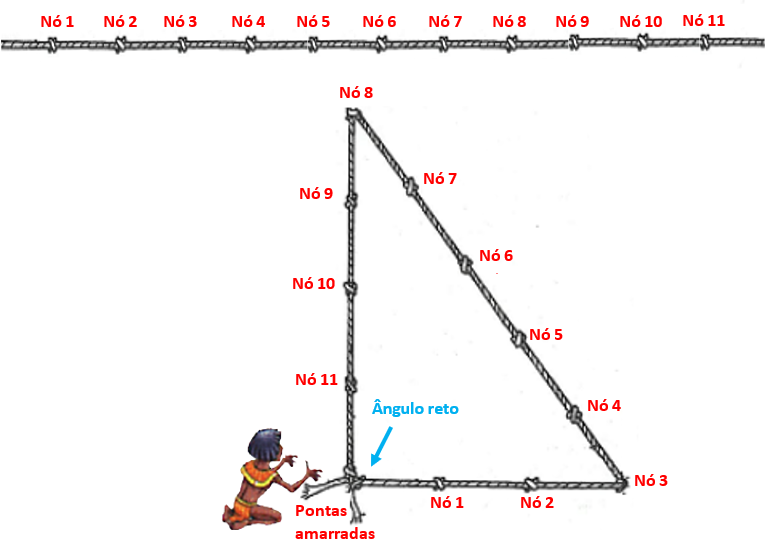
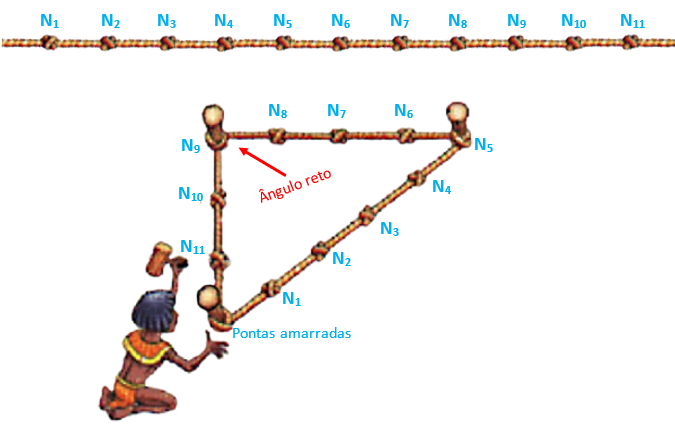
Como não há evidências documentais de que esses egípcios tivessem conhecimento do Teorema de Pitágoras e de sua recíproca, será que há alguma outra forma de mostrar que um “triângulo 3, 4, 5” é retângulo?
Tente, então, garantir a afirmação de que um “triângulo 3, 4, 5” é retângulo utilizando a figura a seguir, a qual aparece no Chou-pei, o mais antigo trabalho chinês conhecido e que remonta ao segundo milênio a.C.


Lembretes
(1) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
(2) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
(3) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes .
(4) Caso de congruência L.L.L. (lado – lado – lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes.
(Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
Solução
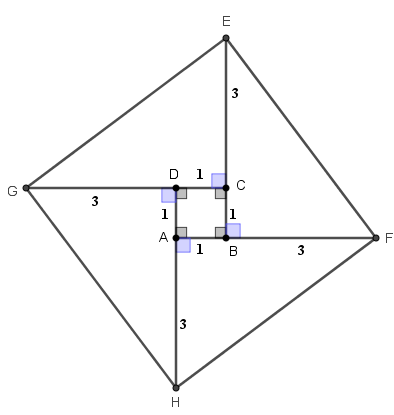
Considere um quadrado ABCD de lado [tex]1[/tex] e prolongue cada lado desse quadrado em [tex]3[/tex] unidades, como mostrado na figura a seguir.
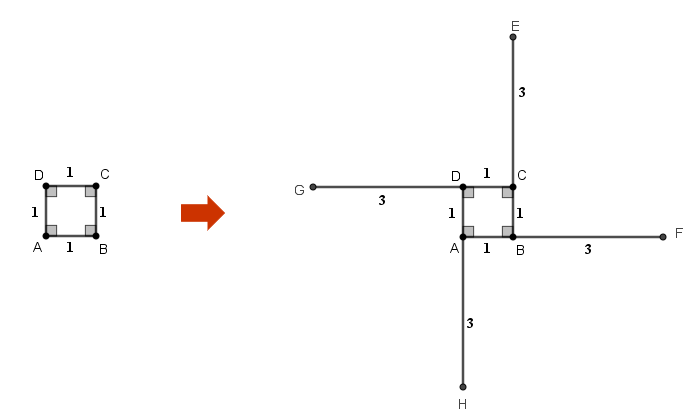
Agora, a partir das extremidades [tex]E[/tex], [tex]F[/tex], [tex]G[/tex] e [tex]H[/tex], trace o quadrilátero [tex]GEFH[/tex].
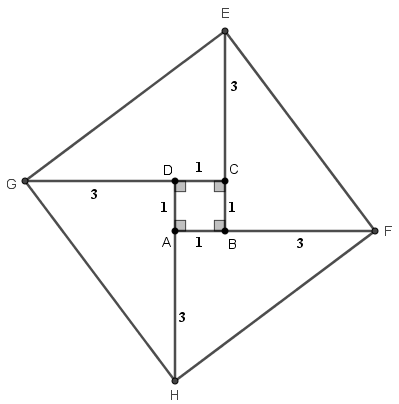
Perceba que temos quatro triângulos retângulos de catetos [tex]4[/tex] e [tex]3[/tex]: [tex]\Delta CGE[/tex], [tex]\Delta BEF[/tex], [tex]\Delta AHF[/tex] e [tex]\Delta GDH[/tex].
Estes triângulos são congruentes pelo caso L.A.L. e, assim, [tex]GEFH[/tex] é um losango.
Além disso, em cada par, os ângulos vermelhos e verdes destacados na figura abaixo são complementares, logo o losango [tex]GEFH[/tex] é um quadrado.
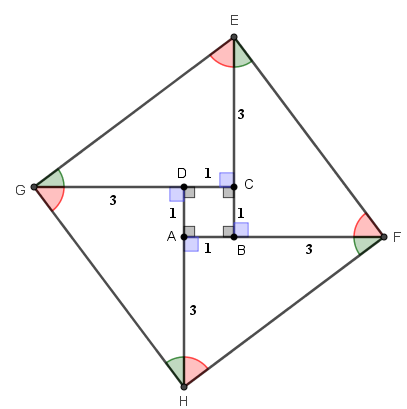
Sejam [tex]S[/tex] e [tex]l[/tex] a área e a medida do lado do quadrado [tex]GEFH[/tex], respectivamente. Como a área de uma figura é a soma das áreas de suas partes, temos que
[tex]\quad\quad S=l^2=1 + 4 \cdot \dfrac{4 \cdot 3}{2}[/tex],
donde [tex] l=5[/tex].
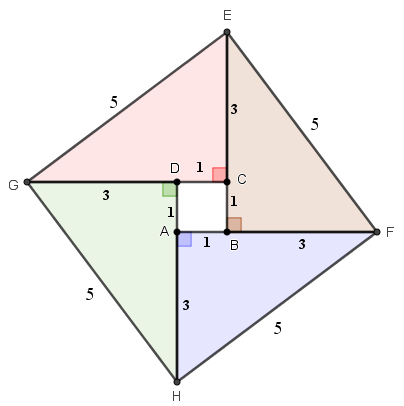
Assim, qualquer triângulo de lados [tex]3[/tex], [tex]4[/tex] e [tex]5[/tex] é congruente aos triângulos [tex]\Delta CGE[/tex], [tex]\Delta BEF[/tex], [tex]\Delta AHF[/tex] e [tex]\Delta GDH[/tex] do problema e, portanto, é um triângulo retângulo.
Solução elaborada pelos Moderadores do Blog .
