Problema
(Indicado a partir do 2º ano do E. M.)
É incrível a velocidade com a qual crescem os números de telefone!
Nos anos da década de [tex]50[/tex], em São Paulo, os telefones possuíam [tex]5[/tex] dígitos.
Atualmente, os telefones de São Paulo já possuem [tex]9[/tex] dígitos.
Suponha que tanto em [tex]1950[/tex] como atualmente todos os algarismos pudessem ser utilizados como dígitos na composição de um número de telefone, exceto o primeiro algarismo, que não pode ser nulo.
Qual seria, então, o aumento na quantidade de números de telefone, entre essas duas épocas?
Solução
Consideradas as condições do problema, vamos contar quantos números de telefone poderiam ser utilizados.
- Em [tex]1950[/tex], para os cinco dígitos teríamos as seguintes escolhas:

- o que nos fornece uma quantidade máxima de [tex]\fcolorbox{black}{#E8E8E8}{$9\cdot 10^4=90\ 000$}[/tex] números de telefone.
- Atualmente, para os nove dígitos teríamos as seguintes escolhas:
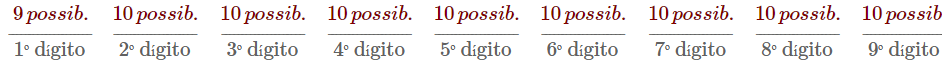
- o que nos fornece uma quantidade máxima de [tex]\fcolorbox{black}{#E8E8E8}{$9\cdot 10^8=900\ 000\ 000$}[/tex] números de telefone.
Dessa forma, o aumento na quantidade de números foi de
[tex]\qquad \fcolorbox{black}{#eee0e5}{$900\ 000\ 000 – 90\ 000=899\ 910\ 000$}[/tex] números.
Solução elaborada pelos Moderadores do Blog.
