Problema
(Indicado a partir do 9º ano do E. F.)
(ITA-2005) Encontre o menor número inteiro [tex]n[/tex] tal que [tex]\sqrt{n}-\sqrt{n-1}\lt 0,01[/tex].
Solução
Do enunciado temos que [tex]\sqrt{n}-\sqrt{n-1}\lt 0,01[/tex]; assim,
[tex]\qquad (\sqrt{n}-\sqrt{n-1})^2\lt( 0,01)^2[/tex]
[tex]\qquad n-2\sqrt{n(n-1)}+n-1\lt 0,0001[/tex]
[tex]\qquad -2\sqrt{n(n-1)}\lt -2n+1+0,0001[/tex]
[tex]\qquad -2\sqrt{n(n-1)}\lt -2n+1,0001. \;\;\;\;\;\;\;\;\;\textcolor{#800000}{(i)}[/tex]
Multiplicando ambos os lados da desigualdade [tex]\textcolor{#800000}{(i)}[/tex] por [tex]-\dfrac{1}{2}[/tex] segue que:
[tex]\qquad \sqrt{n(n-1)}\gt n-0,50005[/tex]
[tex]\qquad (\sqrt{n(n-1)})^2\gt (n-0,50005)^2[/tex]
[tex]\qquad n(n-1)\gt n^2-1,0001n+0,2500500025[/tex]
[tex]\qquad n^2-n\gt n^2-1,0001n+0,2500500025[/tex]
[tex]\qquad -n+1,0001n\gt 0,2500500025[/tex]
[tex]\qquad 0,0001n\gt 0,2500500025[/tex]
[tex]\qquad n\gt \dfrac{0,2500500025}{0,0001}[/tex]
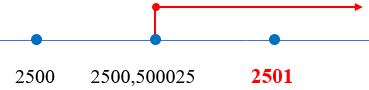
[tex]\qquad n\gt 2500,500025[/tex].
Portanto, o menor inteiro que satisfaz [tex]\sqrt{n}-\sqrt{n-1}\lt 0,01[/tex] é [tex]\, \fcolorbox{black}{#eee0e5}{$n=2501$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
