Problema
(Indicado a partir do 9º ano do E. F.)
É possível, ao redor de uma moeda circular [tex]X[/tex], colocar [tex]n[/tex] moedas idênticas a [tex]X[/tex] que se tangenciam duas a duas e que todas elas tangenciam [tex]X[/tex]?
Em caso afirmativo, o valor de [tex]n[/tex] depende do raio da moeda?
Justifique sua resposta.
Solução
Quando duas circunferências se tangenciam, o ponto de tangência está alinhado com os centros.
Assim, três circunferências de mesmo raio [tex]r[/tex], quando tangentes duas a duas, têm seus centros como vértices de um triângulo equilátero de lado [tex]2r[/tex].
Perceba que os arcos da moeda [tex]X[/tex] com extremidades em dois pontos de tangência com moedas vizinhas serão de [tex]60^{\circ}[/tex], havendo seis desses arcos e, portanto, seis moedas ao redor da moeda [tex]X[/tex], conforme mostramos na figura.
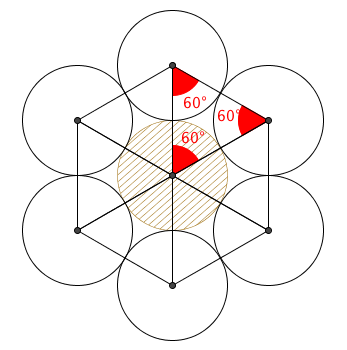
Como fizemos isso para uma moeda circular de raio [tex]r[/tex] qualquer, então o valor de [tex]n[/tex] independe da medida [tex]r[/tex].
Solução elaborada pelos Moderadores do Blog.
Testando a solução
Você pode utilizar o applet abaixo para observar a veracidade da afirmação demonstrada, quantas vezes você quiser!
Basta seguir as instruções e boa diversão!
Instruções:
1) Mova o controle deslizante Raio para definir o raio da moeda X e, consequentemente, das moedas verdes, que são todas idênticas à moeda X.
2) As moedas verdes podem ser movimentadas livremente, basta clicar sobre elas e arrastá-las.
3) Para voltar para a configuração inicial, é só clicar nas setinhas que aparecem no canto superior direito do applet.
1) Mova o controle deslizante Raio para definir o raio da moeda X e, consequentemente, das moedas verdes, que são todas idênticas à moeda X.
2) As moedas verdes podem ser movimentadas livremente, basta clicar sobre elas e arrastá-las.
3) Para voltar para a configuração inicial, é só clicar nas setinhas que aparecem no canto superior direito do applet.
OBMEP_ nzm, criado com o GeoGebra
