Problema
(Indicado a partir do 9º ano do E. F.)
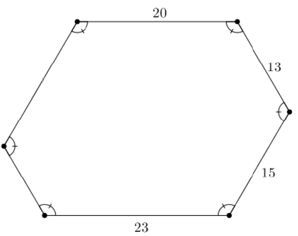
O hexágono da figura é equiângulo.
Se as medidas indicadas estão expressas na mesma unidade de comprimento, encontre os comprimentos dos dois lados que faltam e depois calcule o perímetro do hexágono.
Solução
Para encontrar o perímetro, basta descobrir as medidas dos dois segmentos que faltam. Vamos denotar essas medidas por [tex]x[/tex] e [tex]y[/tex]. Perceba que prolongando os lados de comprimentos [tex]y[/tex], [tex]13[/tex] e [tex]23[/tex] do hexágono construímos três triângulos, já que esses lados não são paralelos entre si.
Pelo fato de o hexágono ser equiângulo, todos os seus ângulos internos medem [tex]120^\circ[/tex] e, consequentemente, os seus ângulos externos medem [tex]60^\circ[/tex] cada um. Portanto, os três triângulos construídos são equiláteros. Veja a figura:
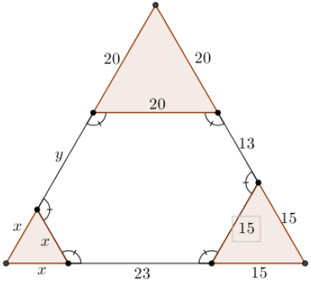
Assim, temos um grande triângulo equilátero de lados com comprimento [tex]48[/tex] e, dessa forma:
- [tex] x+23+15=48 \, [/tex], donde [tex] \, \fcolorbox{black}{#eee0e5}{$x=10$} \, [/tex] unidades de comprimento;
- [tex]20+y+x=48 \, [/tex]; como [tex]x=10[/tex] unidades de comprimento, então [tex] 20+y+10=48[/tex], donde [tex] \, \fcolorbox{black}{#eee0e5}{$y=18$} \, [/tex]unidades de comprimento;
- o perímetro do hexágono vale [tex] \, \fcolorbox{black}{#eee0e5}{$99$} \, [/tex] unidades de comprimento.
Solução elaborada pelos Moderadores do Blog.
