Problema
(Indicado a partir do 2º ano do E. m.)
Um engradado, como o da figura, tem capacidade para 25 garrafas.
Se, de forma aleatória, forem colocadas 5 garrafas no engradado, determine a probabilidade de que quaisquer duas delas não
fiquem numa mesma fila horizontal, nem numa mesma fila vertical.
Solução
- Observe inicialmente que para a primeira garrafa a ser colocada, qualquer um dos 25 lugares podem ser ocupados, de modo que temos 25 casos de interesse, em 25 casos possíveis [tex](\frac{25}{25})[/tex].
- Colocada a primeira garrafa, ficam excluídas todas as possibilidades da linha e da coluna da garrafa colocada, de modo que restam 16 casos de interesse, em 24 casos possíveis [tex](\frac{16}{24})[/tex].
- De modo análogo, para a terceira garrafa teremos 9 casos de interesse em 23 casos possíveis [tex](\frac{9}{23})[/tex].
Para a quarta garrafa, 4 casos de interesse em 22 casos possíveis [tex](\frac{4}{22})[/tex]. - Finalmente, para a última garrafa, apenas um caso de interesse em 21 casos possíveis [tex](\frac{1}{21})[/tex].
Sendo assim, a probabilidade de que quaisquer duas delas não recaiam em uma mesma fila é dada por:
[tex] \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \dfrac{25}{25} \cdot \dfrac{16}{24} \cdot \dfrac{9}{23} \cdot \dfrac{4}{22} \cdot \dfrac{1}{21} = \dfrac{\left(5!\right)^2 \cdot 20!}{25!} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
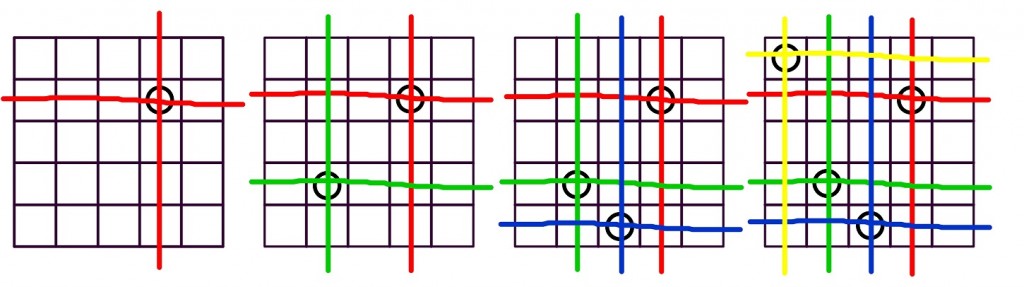
Ajudando a entender . . .
Com a figura abaixo, podemos visualizar uma situação particular do problema e com isso entender melhor o que acontece depois de colocarmos cada uma das quatro primeiras garrafas.
Observe que para a última garrafa não haverá, de fato, opção de escolha.