Problema
(Indicado a partir do 2º ano do E. M.)
(ITA– Adaptado) Sejam [tex]A[/tex] e [tex]B[/tex] dois conjuntos com [tex]6[/tex] e [tex]4[/tex] elementos, respectivamente.
Quantas funções sobrejetivas [tex]f:A\rightarrow B[/tex] existem?
Ajuda

Pelo enunciado do problema, facilmente percebemos que é necessário sabermos o que é uma função sobrejetora, não é?
Poderíamos dizer, simplesmente, que:
- Uma função [tex] f:A \rightarrow B [/tex] é sobrejetora se [tex]Im(f)=B[/tex], ou seja, se seu conjunto imagem for o seu contradomínio.
Mas talvez seja conveniente relembrar o que é o conjunto imagem de uma função e aí sim definir a sobrejetividade, não é?
Então, vamos lá!
É usual definirmos como imagem da função [tex]f[/tex] o conjunto formado pelos elementos de [tex]B[/tex] que são imagens de algum elemento de [tex]A[/tex]. Esse conjunto é indicado por [tex]Im(f)[/tex]; assim:
[tex]\qquad \qquad Im(f)=\{y=f(x)\text{ tais que } x\in A \}[/tex]
e, dado [tex]x \in A[/tex], o elemento único [tex]y \in B[/tex] tal que [tex]y=f(x)[/tex] é dito a imagem de [tex]x [/tex] pela [tex]f.[/tex]
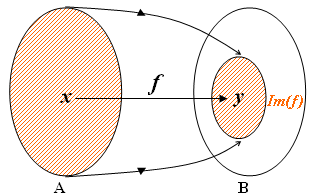
A partir dessa definição, podemos dizer que:
✐ Uma função [tex] f:A \rightarrow B [/tex] é sobrejetora se [tex]Im(f)=B[/tex].
Mas vamos esmiuçar um pouco mais essa definição.
Sabemos que se [tex] f:A \rightarrow B [/tex] é uma função e [tex] \, x \in A[/tex], então a imagem de [tex]x[/tex] pela [tex]f[/tex] é um elemento de [tex]B[/tex], isto é, [tex]y=f(x) \in B[/tex]. Com isso, SEMPRE temos a inclusão [tex]Im(f) \subset B[/tex], conforme sugere a figura acima, independente de [tex]f[/tex] ser ou não sobrejetora.
Então a condição essencial que caracteriza uma função sobrejetora é a de que cada elemento do contradomínio [tex]B[/tex] seja imagem de pelo menos um elemento do domínio. Assim podemos também dizer que:
✐ Uma função [tex] f:A \rightarrow B [/tex] é dita sobrejetora se, para todo [tex]y\in B[/tex], existir um [tex]x\in A[/tex] tal que [tex]f(x)=y[/tex].
Em símbolos:
[tex]\qquad \qquad \forall \, y\in B, \exists \, x\in A[/tex] tal que [tex]y=f(x)[/tex].
Solução
Como temos [tex]6[/tex] elementos no conjunto [tex]A[/tex], [tex]4[/tex] elementos no conjunto [tex]B[/tex] e todo elemento de [tex]B[/tex] deve ser imagem de pelo menos um elemento de [tex]A[/tex], vamos determinar para cada elemento de [tex]B[/tex] quais são os elementos de [tex]A[/tex] dos quais esse elemento é imagem. Para isso, vamos particionar o conjunto [tex]A[/tex] em quatro subconjuntos não vazios e analisar de quantas maneiras essas partições estarão associadas a um elemento de [tex]B[/tex].
A ideia é, primeiramente, separar os elementos de [tex]A[/tex] que terão a mesma imagem e, em seguida, definir qual será essa imagem.
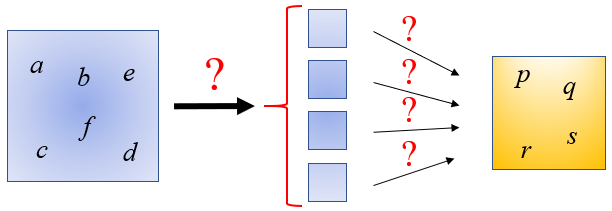
Observe que temos as seguintes formas de realizar a partição:
- Primeira forma: Como [tex]6=2+2+1+1[/tex], podemos agrupar os seis elementos de [tex]A[/tex] em dois conjuntos de dois elementos e dois conjuntos unitários.
- Segunda forma: Como [tex]6=3+1+1+1[/tex], podemos agrupar os seis elementos de [tex]A[/tex] em um conjunto de três elementos e três conjuntos unitários.
O que vamos fazer agora é contar de quantas maneiras podemos distribuir os seis elementos do conjunto [tex]A[/tex] em quatro conjuntos, de modo que cada subconjunto tenha pelo menos um elemento. Nessa contagem, utilizaremos livremente a fórmula de combinação de [tex]m[/tex], [tex]n[/tex] a [tex]n[/tex]:
[tex]\qquad \qquad C_{m,n}=\dfrac{m!}{n!(m-n)!}[/tex]
- A primeira forma de partição pode ser realizada de
- A segunda forma de particionar pode ser realizada de
[tex]\qquad \qquad \dfrac{C_{6,2}\times C_{4,2}}{2} = 45[/tex] maneiras;
pois, definindo quais são os dois conjuntos de dois elementos, os demais conjuntos ficam estabelecidos.
[tex]\qquad \qquad C_{6,3}=20[/tex] maneiras;
pois, definindo o conjunto de três elementos, os demais conjuntos ficam estabelecidos.
Temos, portanto, um total de [tex] \, \fcolorbox{black}{#d7d7d7}{$45+20=65$}[/tex] maneiras de realizar a partição.
[tex]\textcolor{#800000}{(2)}[/tex] Já temos os seis elementos do conjunto [tex]A[/tex] agrupados, resta apenas saber qual será a imagem dos elementos de cada subconjunto.
Perceba que, para cada partição, temos [tex] \, \fcolorbox{black}{#d7d7d7}{$4!=24$}[/tex] maneiras de associar cada conjunto da partição a um, e somente um, dos quatro elementos de [tex]B[/tex].
Assim, como devemos fazer os dois procedimentos:
– agrupar os seis elementos de [tex]A[/tex] em quatro subconjuntos e
– associar uma imagem a cada subconjunto da partição,
o Princípio Fundamental da Contagem (Se você não se lembra desse Princípio, clique AQUI.) nos garante que o total de funções sobrejetivas [tex]f:A\rightarrow B[/tex] é dado por [tex] \, \fcolorbox{black}{#eee0e5}{$65\times 24=1560$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
