Problema
(Indicado a partir do 1º ano do E. M.)
A imagem a seguir mostra o gráfico de uma função real [tex]f[/tex].
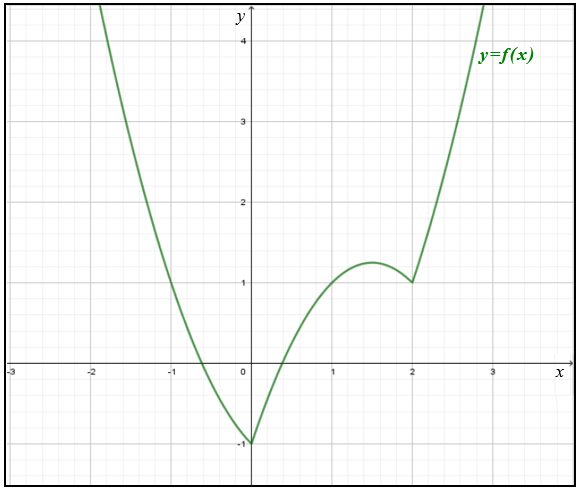
Quantas soluções reais possui a equação [tex]|f(x)|=1[/tex] no intervalo fechado [tex]\left[-\frac{3}{2},\frac{5}{2}\right][/tex]?
Solução
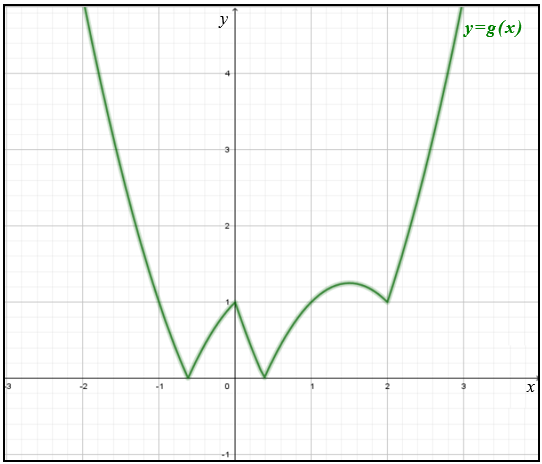
Conhecendo o gráfico da [tex]f[/tex], podemos esboçar o gráfico da função [tex]g[/tex] definida por [tex]g(x)=|f(x)|.[/tex] Particularmente, nos interessará o gráfico no intervalo [tex]\left[-\frac{3}{2},\frac{5}{2}\right][/tex].
Como [tex]g(x)=f(x)[/tex], se [tex]f(x)\geq0[/tex], e [tex]g(x)=-f(x)[/tex], se [tex]f(x)\lt 0[/tex], então:
- nos intervalos em que [tex]f(x)\geq0[/tex], o gráfico da função [tex]g[/tex] será igual ao da [tex]f[/tex];
- nos intervalos em que [tex]f(x)\lt 0[/tex], para obter o gráfico de [tex]g[/tex] devemos refletir o gráfico de [tex]f[/tex] em relação ao eixo [tex]x[/tex].
Para encontrarmos quantas soluções a equação [tex]|f(x)|=1[/tex] possui, basta contarmos quantas vezes a função [tex]g[/tex] assumiu o valor [tex]1[/tex] no intervalo [tex]\left[-\frac{3}{2},\frac{5}{2}\right][/tex] e para isso:
- basta contarmos quantas são as interseções do gráfico de [tex]g[/tex] com a reta [tex]y=1[/tex] no intervalo [tex]\left[-\frac{3}{2},\frac{5}{2}\right][/tex].
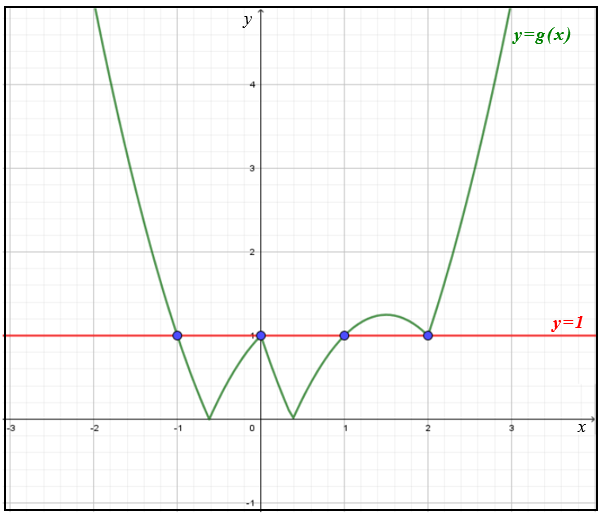
Portanto, a equação [tex]|f(x)|=1[/tex] possui [tex]\, \fcolorbox{black}{#eee0e5}{$4 \text{ soluções}$}[/tex] no intervalo fechado [tex]\left[-\frac{3}{2},\frac{5}{2}\right].[/tex]
Solução elaborada pelos Moderadores do Blog.
