Problema
(Indicado a partir do 9º ano do E. F.)
Uma folha de papel retangular medindo [tex]4[/tex] unidades de comprimento e [tex]3[/tex] unidades de altura foi dobrada ao longo da linha tracejada indicada na figura. Determine a área do triângulo sombreado.
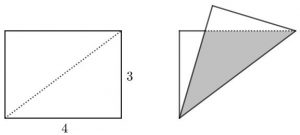
Extraído de XV Gara Nazionale di Matematica, 1999.
Solução
Observe a figura abaixo e note que os triângulos [tex]ABE[/tex] e [tex]CDE[/tex] são congruentes pelo caso LAA.
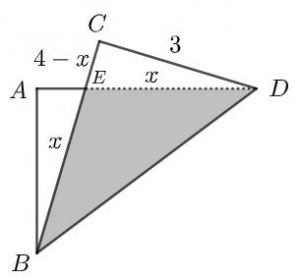
De fato, podemos ver que
[tex]\qquad E\hat{C}D=E\hat{A}B=90^\circ,[/tex]
e, por serem opostos pelo vértice,
[tex]\qquad D\hat{E}C=B\hat{E}A. [/tex]
Agora, devido ao fato que os ângulos de um triângulo somarem [tex]180^\circ[/tex], temos
[tex]\qquad E\hat{D}C=E\hat{B}A.[/tex]
Temos também a igualdade dos lados correspondentes [tex]AB=CD=3[/tex].
Com isso, podemos concluir que [tex]BE=DE=x[/tex] e [tex]AE=CE=4-x[/tex].
Aplicando o Teorema de Pitágoras no triângulo retângulo [tex]ECD[/tex], temos
[tex]\qquad (4-x)^2+3^2=x^2[/tex]
[tex]\qquad 16-8x+x^2+9=x^2[/tex]
[tex]\qquad 25=8x [/tex]
[tex]\qquad x=\dfrac{25}{8}.[/tex]
No triângulo sombreado, vamos usar [tex]\overline{BE}[/tex] como base e [tex]\overline{CD}[/tex] como altura. Dessa maneira, a área deste triângulo é
[tex]\qquad \dfrac{1}{2}\cdot BE\cdot CD=\dfrac{1}{2} \cdot \dfrac{25}{8}\cdot 3=\dfrac{75}{16}.[/tex]
Solução elaborada pelos Moderadores do Blog.
