Problema
(Indicado a partir do 8º ano do E. F.)
As três fitas que aparecem na figura têm uma mesma largura horizontal constante [tex]a[/tex]. Essas três fitas conectam duas linhas paralelas.
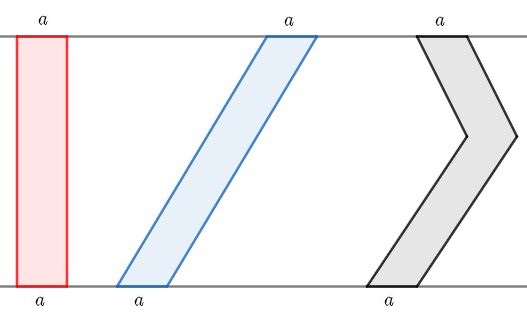
Observando as fitas, cinco amigos fizeram as seguintes observações:
- André: É impossível saber qual fita tem maior área sem conhecer a medida [tex]a[/tex];
- Andreia: A fita vermelha tem maior área;
- Raquel: A fita azul tem maior área;
- Ronan: A fita cinza tem maior área;
- Susane: Todos vocês erraram…
Qual amigo está correto?
Adaptado da EUROPEAN ‘KANGAROO’ MATHEMATICAL CHALLENGE ‘PINK’ – 2003.
Lembrete
✏ A área de um paralelogramo pode ser calculada pelo produto da medida de sua base pela medida de sua altura.
Solução
A partir da figura, traçamos outra reta paralela de forma a dividir a fita cinza em dois paralelogramos. Indicamos as distâncias entre as retas como [tex]b[/tex] e [tex]c[/tex].
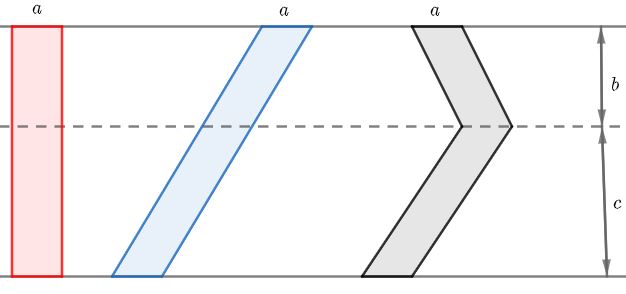
As fitas vermelha e azul são paralelogramos de base [tex]a[/tex] e altura [tex]b+c[/tex] (lembre-se, um retângulo é um caso especial de paralelogramo!). Logo, suas áreas são ambas iguais a [tex]a\cdot(b+c)[/tex]. Assim:
- [tex]\textcolor{red}{A_{verm}=a\cdot(b+c)}[/tex];
- [tex]\textcolor{blue}{A_{azul}=a\cdot(b+c)}[/tex].
Perceba que a fita cinza ficou dividida em dois paralelogramos de base [tex]a[/tex] e alturas [tex]b[/tex] e [tex]c[/tex], respectivamente. Logo, sua área é dada pela soma das áreas desses paralelogramos, ou seja, também vale [tex]a\cdot b+a\cdot c[/tex] e assim
- [tex]\textcolor{gray}{A_{cinza}=a\cdot(b+c)}[/tex].
Dessa forma, Susane estava correta: Todas as fitas têm a mesma área e os quatro primeiros amigos se confundiram.
Aprofundando um pouco mais!
Você pode estar se perguntando:
– Mas, o que garante que a reta que passa pelos dois pontos do “cotovelo” da fita cinza é paralela às retas paralelas iniciais?
Vamos analisar melhor a fita cinza, dando nomes a alguns pontos:
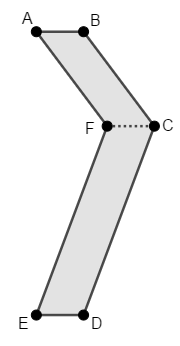
Na solução, ao traçarmos a terceira paralela, quando afirmamos que dividiríamos a fita cinza em dois paralelogramos, estávamos supondo implicitamente que [tex]\overline{FC}[/tex] é um segmento paralelo aos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{ED}[/tex]. Temos certeza disso?
Vejamos!
O enunciado garante que as três fitas têm a mesma largura horizontal constante [tex]a[/tex]. Então, “entre um cotovelo e outro”, os lados da fita cinza são paralelos! De fato, esta é uma das características exclusivas das retas paralelas: a distância entre elas é sempre a mesma.
Suponhamos que temos os segmentos [tex]\overline{AB},\overline{BC}[/tex] e [tex]\overline{CD}[/tex] e queremos construir a fita cinza de maneira que a largura seja constante. Podemos fazer isso simplesmente traçando a paralela a [tex]\overline{AB}[/tex] passando por [tex]C[/tex] e medindo à esquerda de [tex]C[/tex] o tamanho [tex]a[/tex]. Marcamos o ponto [tex]F[/tex] e ficamos com a fita [tex]ABCDEF[/tex], formada pelos paralelogramos [tex]ABCF[/tex] e [tex]FCDE[/tex]. Como na solução que fizemos!
O que precisamos ter certeza é que não podemos construir outra fita cinza com estas condições (segmentos [tex]\overline{AB},\overline{BC}[/tex] e [tex]\overline{CD}[/tex] e largura constante!)!! Bem, como a largura deve ser constante, concluímos que a reta [tex]AF[/tex] é exatamente a única reta paralela a [tex]\overline{BC}[/tex] que passa por [tex]A[/tex], enquanto [tex]FE[/tex] é exatamente a única reta paralela a [tex]\overline{CD}[/tex] que passa por [tex]E[/tex]. (Aqui usamos o chamado postulado das paralelas: “Por um ponto fora de uma reta não se pode traçar mais que uma reta paralela à reta dada”. Esta interessante afirmação da Geometria Euclidiana, ou seja, da geometria que aprendemos na escola, baseia-se no quinto postulado de Euclides, enunciado no livro Elementos de Euclides.)
Como as retas são únicas, há um único ponto possível para ser o ponto [tex]F[/tex], que é a interseção dessas retas. Logo, o [tex]F[/tex] só pode ser o ponto que construímos anteriormente, isto é, aquele tal que a fita [tex]ABCDEF[/tex] é formada pelos paralelogramos [tex]ABCF[/tex] e [tex]FCDE[/tex].
Que bom que deu certo!!
Solução elaborada pelos Moderadores do Blog.
