✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
(ENEM 2016, 2ª aplicação – Adaptado) Admita que um tipo de eucalipto tenha expectativa de crescimento exponencial, nos primeiros anos após seu plantio, modelado pela função [tex]y[/tex] definida por [tex]\boxed{y(t) = a^{t-1}}[/tex], na qual [tex]y[/tex] representa a altura da planta em metro, [tex]t[/tex] é considerado em ano, e [tex]a[/tex] é uma constante maior que [tex]1[/tex].
O gráfico abaixo representa a função [tex]y[/tex].
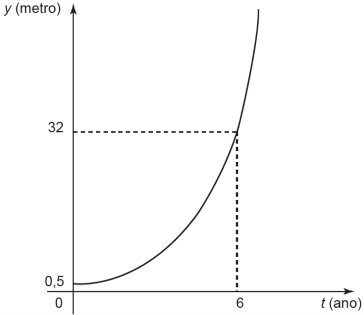
Admita ainda que [tex]y(0)[/tex] fornece a altura da muda quando plantada, e deseja-se cortar os eucaliptos quando as mudas crescerem [tex]7,5 ~m[/tex] após o plantio.
Determine, em anos, o tempo decorrido entre a plantação e o corte.
Solução
Inicialmente, destacamos no gráfico apresentado dois pontos que poderão ser utilizados na resolução.
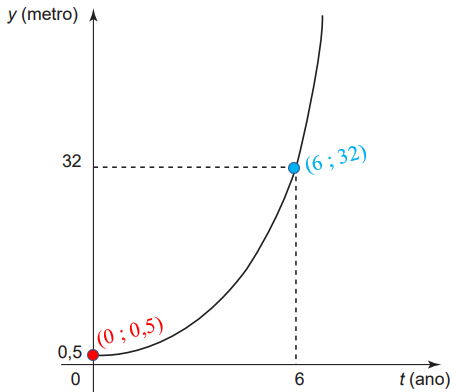
Observe que:
- analisando o gráfico, segue que [tex]\boxed{y(0)=0,5}[/tex];
- utilizando a definição da função [tex]y[/tex], temos [tex]\boxed{y(0)=a^{0-1}=\dfrac{1}{a_\;}}.[/tex]
Com isso, concluímos que
[tex]\qquad \dfrac{1}{a}=0,5=\dfrac{1}{2}[/tex],
ou seja, [tex]a = 2[/tex] e, portanto, [tex]\boxed{y(t) = 2^{t-1}}\,.[/tex]
Como deseja-se cortar os eucaliptos quando as mudas crescerem [tex]7,5 ~m[/tex] após o plantio, então eles serão cortados quando atingirem [tex]0,5+7,5=8 ~m[/tex] de altura.
Sendo [tex]t[/tex] o tempo decorrido até o corte do eucalipto, segue que:
[tex]\qquad y(t) = 8 \\
\qquad 2^{t-1} = 8\\
\qquad 2^{\textcolor{red}{t-1}} = 2^\textcolor{red}{3} \\
\qquad \textcolor{red}{t-1} = \textcolor{red}{3}\\
\qquad t = 4.[/tex]
Logo, o tempo decorrido entre a plantação e o corte dos eucaliptos é de [tex]4[/tex] anos.
Solução elaborada pelos Moderadores do Blog.
