✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2º ano do E. M.)
Em um campo de futebol, a marca do pênalti fica centralizada a [tex]11[/tex] m de distância da linha do gol, que tem altura de [tex]2,44[/tex] m e largura de [tex]7,32[/tex] m, como mostra a figura [tex]1[/tex].
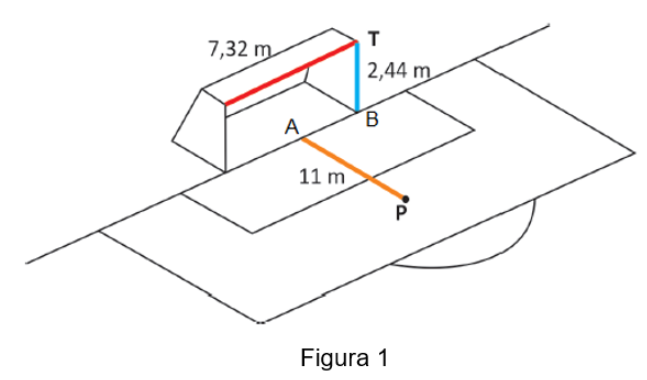
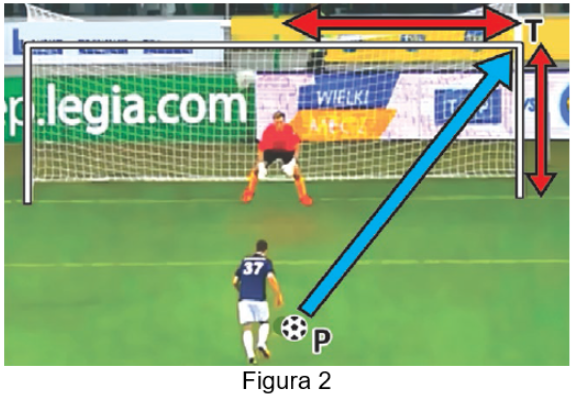
Um jogador, ao bater um pênalti do ponto [tex]P[/tex] (figura [tex]2[/tex]), em um jogo de futebol, acertou o travessão exatamente no ponto [tex]T[/tex], ângulo superior à esquerda do goleiro.
(Dado: [tex]3,66^2+2,44^2 \approx 19[/tex])
Responda:
a) Para que a bola percorra a menor distância até o gol, o jogador deveria ter chutado na direção do ponto [tex]A[/tex] ou do ponto [tex]T[/tex]?
b) Considerando que o goleiro está posicionado exatamente no meio da linha da trave, ponto [tex]A[/tex], qual a distância entre os pontos [tex]A[/tex] e [tex]B[/tex]?
c) Qual a distância entre os pontos [tex]P[/tex] e [tex]B[/tex]?
d) Qual a distância [tex]d[/tex] percorrida pela bola de [tex]P[/tex] a [tex]T[/tex], ou seja, a distância do chute até tocar a trave no ângulo reto?
(Extraído do livro Matemática, volume único– Gelson Iezzi & outros)
Solução
a) Observe a figura.
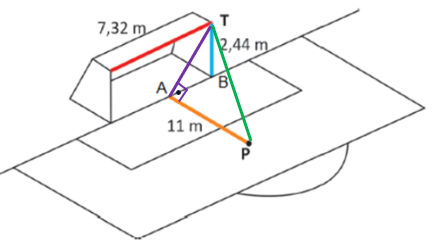
A distância de [tex]A[/tex] a [tex]P[/tex] é a menor ao gol por se tratar de um cateto do triângulo retângulo [tex]TAP[/tex].
b) Como o goleiro está posicionado no meio do gol, a distância pedida é [tex]7,32 \div 2=3,66 \ m.[/tex]
c) Observe a figura.
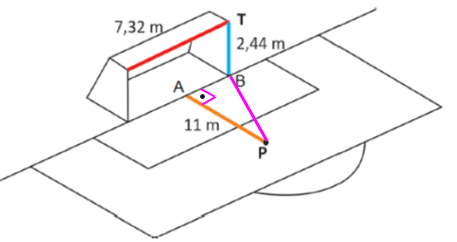
Aplicando o Teorema de Pitágoras no triângulo [tex]PAB[/tex], temos:
[tex]\qquad {PB}^2={PA}^2+{AB}^2 \\
\qquad {PB}^2=11^2+\left(\dfrac{7,32}{2}\right)^2\\
\qquad {PB}^2=121+13,3956=134,3956\\
\qquad {PB}\approx 11,59 \ m.[/tex]
d) Aplicando o Teorema de Pitágoras no triângulo [tex]ABT[/tex] da figura do item (a), temos:
[tex]\qquad {AT}^2={AB}^2+{BT}^2 \\
\qquad {AT}^2=3,66^2+2,44^2=19,3492\\
\qquad AT \approx \sqrt{19} \ m.[/tex]
Agora, aplicando o Teorema de Pitágoras no triângulo [tex]PAT[/tex] da figura do item (a), segue que:
[tex]\qquad {PT}^2={AT}^2+{AP}^2\approx(\sqrt{19})^2+11^2=140\\
\qquad {PT} \approx 11,8 \ m.[/tex]
Solução elaborada pelos Moderadores do Blog.
