Problema
(Indicado a partir do 1º ano do E. M.)
Encontre um ponto [tex]P[/tex] na hipotenusa [tex]\overline{AB}[/tex] de um triângulo retângulo [tex]ABC[/tex] de modo que a soma dos quadrados das distâncias de [tex]P[/tex] a [tex]\overline{AC}[/tex] e a [tex]\overline{BC}[/tex] seja mínima.
Solução
Sejam [tex]M[/tex] e [tex]N[/tex] os pés dos segmentos que definem as distâncias de [tex]P[/tex] a [tex]\overline{AC}[/tex] e a [tex]\overline{BC}[/tex], respectivamente.
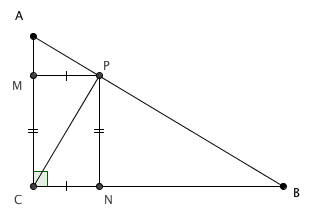
Notamos que [tex]PMCN[/tex] é um retângulo; portanto, seus lados opostos são congruentes.
Pelo teorema de Pitágoras, temos, então, que [tex] PM^2 + PN^2 = CP^2[/tex]; assim a soma dos quadrados das distâncias será mínima quando [tex]CP^2[/tex] for mínimo, ou seja, quando [tex]CP[/tex] for mínimo, o que ocorre se, e somente se, [tex]\overline{CP}[/tex] for perpendicular a [tex]\overline{AB}[/tex]
(Lembre-se de que a distância de um ponto [tex]X[/tex] a uma reta [tex]r[/tex] é obtida por meio da reta perpendicular a [tex]r[/tex] que passa pelo ponto [tex]X[/tex]).
Logo, o ponto [tex]P[/tex] procurado é o pé da altura do triângulo relativa à hipotenusa.
Solução elaborada pelos Moderadores do Blog.
Visualização do problema e da solução
Para ajudar na visualização do problema e de sua solução, utilize o applet disponibilizado abaixo.
1) Aguarde o arquivo carregar.
2) Movimente o ponto [tex]B[/tex] para modificar o tamanho do triângulo retângulo [tex]ABC[/tex].
3) Movimente o ponto [tex]P[/tex] para obter várias simulações do valor a ser minimizado.
✏ Para movimentar um ponto, clique nele com o botão esquerdo do mouse, mantenha o botão apertado e, em seguida, movimente o mouse.
4) Para cada ponto [tex]P[/tex] escolhido, o valor da medida a ser minimizada aparece na parte inferior do applet , juntamente com a medida em graus do ângulo entre [tex]\overline{CP}[/tex] e a [tex]\overline{AB}[/tex].
5) Clique nas setinhas que aparecem no canto superior direito do applet, para voltar à configuração inicial.
OBMEP_ srdg, criado com o GeoGebra
Observamos que a planilha ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
