Problema
(Indicado a partir do 1º ano do E. M.)
Utilizando apenas um esquadro e um lápis, como encontrar o centro de um círculo de diâmetro menor do que o maior lado do esquadro?
Lembrete
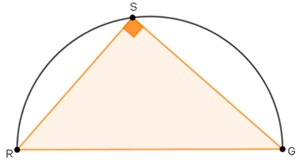
✏ O arco correspondente a um ângulo reto inscrito em uma circunferência é uma semicircunferência.
Solução
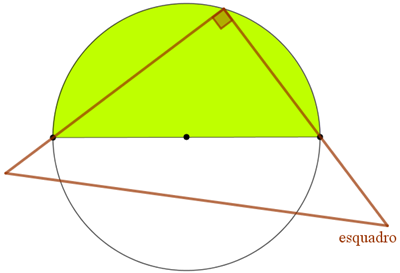
- Observe que, posicionando um esquadro de modo que o vértice do ângulo reto esteja sobre uma circunferência e os catetos fiquem secantes a ela, teremos um ângulo inscrito reto que subtenderá uma semicircunferência.
Assim, se executarmos duas vezes esse procedimento utilizando os pontos [tex]A[/tex] e [tex]A_1[/tex] do círculo em questão como vértices do ângulo reto do esquadro, obteremos a figura abaixo, na qual os segmentos [tex]\overline{DE}~[/tex] e [tex]~\overline{FG}~[/tex] são diâmetros do círculo. Então, o centro deste círculo será o ponto [tex]O[/tex], interseção de [tex]\overline{DE}~[/tex] e [tex]\overline{FG}.[/tex]
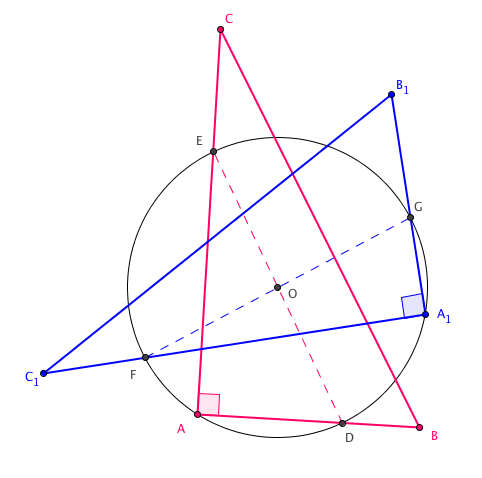
Solução elaborada pelos Moderadores do Blog.
Faça você mesmo
Utilize o aplicativo abaixo para testar a solução do problema.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Escolha uma medida para o raio do círculo. Para isso clique no ponto preto r com o botão esquerdo do mouse, mantenha o botão pressionado e movimente-o horizontalmente. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e movimentá-lo.)
(3) Obtenha um esquadro, clicando no quadradinho Esquadro.
– Para transladar o esquadro obtido, basta clicar sobre ele com qualquer botão do mouse, manter o botão pressionado e fazer o movimento.
– Para rodar o esquadro, clique com o botão esquerdo do mouse sobre o vértice identificado com um pequeno círculo, mantenha o mouse pressionado e faça a rotação.
(Se você estiver utilizando um celular ou um tablet, basta tocar levemente no esquadro ou no vértice e fazer os respectivos movimentos.)
(4) Posicione o esquadro de modo que o vértice do ângulo reto fique sobre a circunferência do círculo e os catetos fiquem secantes à circunferência.
(5) Clique no quadradinho Pontos D e E para obter dois pontos sobre a circunferência. Posicione esses pontos nas interseções dos catetos do esquadro com a circunferência; para isso, clique sobre cada um deles com qualquer botão do mouse e rode o ponto sobre a circunferência. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente nos pontos e movimentá-los.)
(6) Clique no quadradinho Segmento DE para obter o diâmetro [tex]\overline{DE}~[/tex].
(7) Posicione, agora, o esquadro de modo que o vértice do ângulo reto fique sobre um outro ponto da circunferência e os catetos fiquem secantes a ela.
(8) Clique no quadradinho Pontos F e G para obter mais dois pontos sobre a circunferência. Posicione esses pontos nas interseções dos catetos do esquadro com a circunferência.
(9) Clique no quadradinho Segmento FG para obter o diâmetro [tex]\overline{FG}~[/tex].
(10) Esconda o esquadro, desmarcando o quadradinho Esquadro.
(11) Clique no quadradinho Centro do círculo e observe que esse ponto corresponde à interseção dos segmentos [tex]\overline{DE}~[/tex] e [tex]~\overline{FG}.[/tex]
(12) Clique nas setinhas circulares que aparecem no canto superior direito da telinha do aplicativo para voltar à configuração inicial e repita o processo quantas vezes você quiser!
(13) Observamos que o aplicativo fornece uma construção aproximada do processo.
OBMEP_ srdg, criado com o GeoGebra
