Problema
(Indicado a partir do 1º ano do E. M.)
Na figura abaixo, o ângulo [tex]Q\hat {P}R[/tex] mede [tex]45^\circ[/tex]. Os segmentos [tex] \overline {QS}[/tex] e [tex] \overline {RS}[/tex] prolongados são perpendiculares a [tex] \overline {PR}[/tex] e [tex] \overline {PQ}[/tex], respectivamente.
Sabendo que [tex] PS=20 \, cm[/tex], calcule a distância do ponto [tex]Q[/tex] ao ponto [tex]R[/tex].
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex] \overline {AB}[/tex] e o seu comprimento por [tex]AB[/tex].
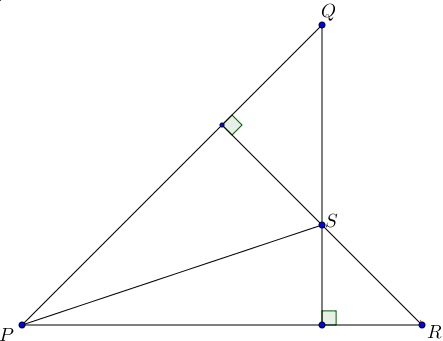
Solução
Utilizando os dados do enunciado, obtemos a figura a seguir, na qual denotaremos por [tex]x[/tex] a distância desejada.
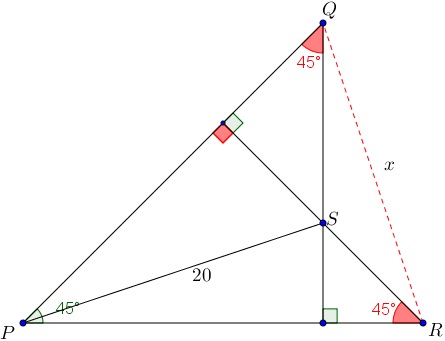
Sabendo que a soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ [/tex], podemos encontrar a medida de outros ângulos indicados na próxima figura.
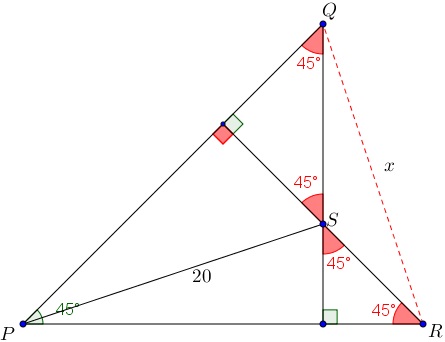
Seja [tex]T[/tex] o ponto de interseção do prolongamento do segmento [tex] \overline {RS}[/tex] com o segmento [tex] \overline {PQ}[/tex]. Note que os triângulos [tex]TQS[/tex] e [tex]TPR[/tex] são isósceles, com [tex]TQ = TS[/tex] e [tex]TP = TR[/tex].
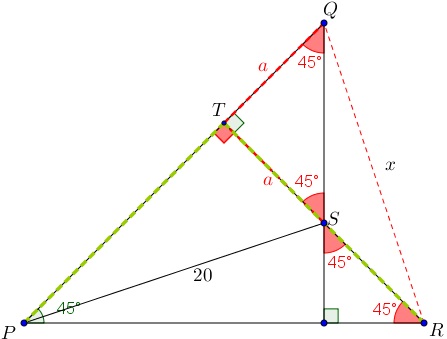
Por fim, repare que o triângulo [tex]PTS[/tex] é congruente com o triângulo [tex]RTQ[/tex] pelo caso [tex]LAL[/tex] (O segmento [tex] \overline {PT}[/tex] é congruente ao segmento [tex] \overline {RT}[/tex], ambos possuem ângulo reto em [tex]T[/tex] e o segmento [tex] \overline {TS}[/tex] é congruente ao segmento [tex] \overline {TQ}[/tex]) .
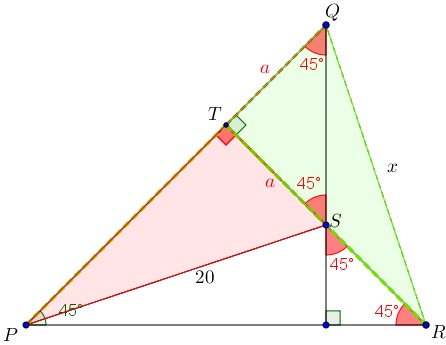
Pela congruência dos triângulos [tex]PTS[/tex] e [tex]RTQ[/tex], concluímos que [tex] \, \fcolorbox{black}{#eee0e5}{$x=20 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
