Problema
(Indicado a partir do 1º ano do E. M.)
A deficiência de fósforo nos solos brasileiros se manifesta na baixa produtividade. Para reverter esse problema, uma equipe de agrônomos acompanhou a lavoura de um grupo de pequenos produtores, de modo a obter uma relação entre a produção [tex]S[/tex] de soja, em quilogramas por hectare [tex](kg/ha)[/tex], e a quantidade [tex]n[/tex] de [tex]P_2O_5[/tex] aplicada no solo, em [tex]kg/ha[/tex], e obteve a seguinte lei:
Segundo essa lei, qual a produção máxima de soja que pode ser obtida, associada à aplicação de [tex]P_2O_5[/tex] no solo?
Adaptado de Insper 2019 – 1º Ano.

Lembretes
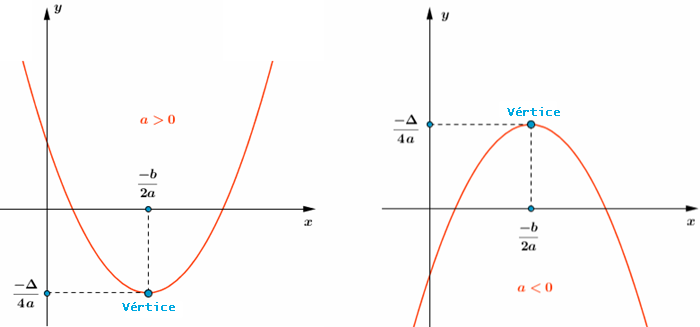
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução 1
A função dada para a produção de soja [tex]S(n)[/tex] é uma função quadrática da forma [tex]ax^2+bx+c[/tex], com
Essa função representa uma parábola voltada para baixo (pois o coeficiente de [tex]a[/tex] é negativo), e a produção máxima de soja ocorre no vértice dessa parábola.
Para encontrar o valor de [tex]n[/tex] que maximiza [tex]S(n) [/tex], podemos usar a fórmula do vértice para uma função quadrática, que é dada por:
Substituindo [tex]b[/tex] e [tex]a[/tex], temos: [tex]n=-\dfrac{2}{2\cdot (-0,05)}=240.[/tex]
Portanto, a quantidade de [tex]P_2O_5[/tex] que maximiza a produção de soja é [tex]n=240\ kg/ha.[/tex]
Agora, aplicamos [tex]n=240[/tex] na função [tex]S(n) [/tex] para obter a produção máxima:
[tex]\qquad S(240)=900+24\cdot (240)–0,05\cdot (240)^2[/tex]
[tex]\qquad S(240)=900+5\ 760–0,05\cdot 57\ 600[/tex]
[tex]\qquad S(240)=900+5\ 760–2\ 880=3\ 780\ kg/ha.[/tex]
Portanto, a produção máxima de soja que pode ser obtida é de [tex]3\ 780\ kg/ha[/tex], associada à aplicação de [tex]240\ kg/ha[/tex] de [tex]P_2O_5[/tex] no solo.
Solução elaborada pelo COM Potências de Euler.
Solução 2
Como [tex]S[/tex] representa a produção de soja, logo devemos determinar o [tex]y_v[/tex]. Assim sendo, pela lei da função, temos que [tex]a=-0,05=-\frac{1}{20}[/tex], [tex]b=24, c=900[/tex].
Para determinar o [tex]\Delta[/tex], faremos: [tex]\Delta=b^2-4ac=24^2-4\cdot (-\frac{1}{20}) \cdot 900=756.[/tex]
Usando a fórmula do [tex]y_v[/tex], encontramos: [tex]y_v=\frac{-\Delta}{4a}=\frac{-756}{4\cdot\left(-\frac{1}{20}\right)}=3\ 780.[/tex]
Portanto, a quantidade máxima de soja é dada por [tex]3\ 780\ kg/ha[/tex].
Uma informação interessante é que, ao determinar o [tex]x_v[/tex], encontramos a quantidade de [tex]P_2O_5[/tex] que deve ser utilizada para termos a produção máxima, que, nesse caso, é [tex]x_v=\frac{-b}{2a}=\dfrac{-24}{2\cdot \left(-\frac{1}{20}\right)}=240\ kg/ha.[/tex]
Solução elaborada pelo COM Phidias.