.Problema de Olimpíada: Frações de Dominó

Problema

---

Se ignorarmos o “duplo zero”, as restantes [tex]27[/tex] peças de um jogo de dominó podem ser vistas como frações inferiores ou iguais a 1. Observe o exemplo abaixo.

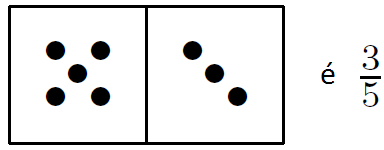
Qual a soma dessas [tex]27[/tex] frações?

(OLIMPÍADA DE MATEMÁTICA DO ESTADO DO RIO DE JANEIRO – 2011.)

Solução

---

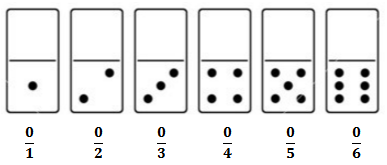
Para obter essa soma, basta que somemos as [tex]21[/tex] frações correspondentes às peças que não contém nenhum zero, já que as frações [tex]\dfrac{0}{1}, \, \dfrac{0}{2}, \, \dfrac{0}{3}, \, \dfrac{0}{4}, \, \dfrac{0}{5}, \, \dfrac{0}{6}[/tex] correspondem ao número zero que, como parcela, não altera uma soma.

Vamos, então, à soma:

[tex]\dfrac{1}{1}+\left(\dfrac{1}{2}+\dfrac{2}{2}\right)+ \left(\dfrac{1}{3}+\dfrac{2}{3}+\dfrac{3}{3}\right)+ \left(\dfrac{1}{4}+\dfrac{2}{4}+\dfrac{3}{4}+\dfrac{4}{4}\right)+\\
\qquad + \left(\dfrac{1}{5}+\dfrac{2}{5}+\dfrac{3}{5}+\dfrac{4}{5}+\dfrac{5}{5}\right)+ \left(\dfrac{1}{6}+\dfrac{2}{6}+\dfrac{3}{6}+\dfrac{4}{6}+\dfrac{5}{6}+\dfrac{6}{6}\right)=\\
\qquad = 1+\dfrac{3}{2}+2+\dfrac{5}{2}+3+\dfrac{7}{2}=\\
\qquad =\dfrac{27}{2}[/tex].
Assim, a soma das [tex]27[/tex] frações de dominó é [tex]\dfrac{27}{2}[/tex].

---

Solução elaborada pelos Moderadores do Blog.