.Problema de Gincana: Uma mistura de vinho

Problema

Um garrafão contém [tex]p[/tex] litros de vinho.
Retira-se um litro de vinho do garrafão e acrescenta-se um litro de água, obtendo-se uma mistura homogênea; retira-se, a seguir, um litro da mistura e acrescenta-se um litro de água e assim sucessivamente.
Quantos litros de vinho restarão no garrafão após [tex]n[/tex] operações?

a) [tex]\dfrac{(p-1)^n}{p^{n+1}}\,\,\,\,[/tex].

b) [tex]\dfrac{(p-1)^n}{p^{n-1}}[/tex].

c)[tex]\dfrac{(p-1)^{n-1}}{p^{n}}[/tex].

d) [tex]\dfrac{p^{n-1}}{(p-1)^{n}}[/tex].

e) [tex]\dfrac{p^{n-1}}{(p + 1)^{n}}[/tex].

Solução 1

Resposta: Alternativa B
Justificativa: Supondo que a solução é homogênea, após cada etapa é retirado [tex]\dfrac{1}{p}[/tex] do volume de vinho. Sendo assim, o volume de vinho após cada etapa será o volume da etapa anterior multiplicado por [tex]\left(1-\dfrac{1}{p} \right)[/tex], ou seja, os volumes de vinho formam uma P.G. cujo primeiro termo é [tex]p[/tex] e a razão, [tex]\left( 1-\dfrac{1}{p} \right)[/tex].

Após [tex]n[/tex] operações, teremos

[tex]\qquad\qquad V_{n+1} = p \cdot \left( 1-\dfrac{1}{p} \right)^n[/tex]

[tex]\qquad\qquad V_{n+1} = p \cdot \left( \dfrac{p-1}{p} \right)^n[/tex]

[tex]\qquad\qquad V_{n+1} = \dfrac{(p-1)^n}{p^{n-1}}[/tex].

Solução elaborada pelos Moderadores do Blog.

Solução 2

Para você que não sabe o que é uma P.G. ou, simplesmente, não entendeu a solução anterior, vamos explicitar os cálculos.

• A princípio, havia [tex]p[/tex] litros de vinho no garrafão. Vamos indicar esse volume de vinho por [tex]V_1[/tex]; assim:
  [tex]\qquad \textcolor{#BC00BC}{\boxed{V_1=p}}.[/tex]



• Foi, então, retirado um litro desse vinho e acrescentado um litro de água no garrafão. Não precisamos fazer cálculos sofisticados para concluir que, após essa primeira retirada, obteve-se uma mistura homogênea de vinho e água na qual existe um total de [tex]p-1[/tex] litros de vinho. Vamos indicar esse volume de vinho por [tex]V_2[/tex]; logo:
  [tex]\qquad \textcolor{#BC00BC}{\boxed{V_2=\left(p-1\right)}}.[/tex]
  
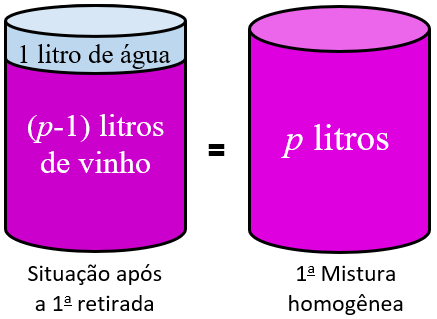
• Dessa primeira mistura homogênea, retirou-se um litro e foi acrescentado um litro de água.
  Para determinarmos a quantidade de vinho presente nessa segunda mistura homogênea de [tex]p[/tex] litros, vamos precisar fazer alguns cálculos. Para isso, utilizaremos uma regra de três simples: se após a retirada de [tex]1[/tex] litro da mistura de [tex]p[/tex] litros sobraram [tex]p-1[/tex] litros dessa mistura, qual o correspondente volume [tex]V_3[/tex] que sobrou dos [tex]p-1[/tex] litros de vinho presentes na mistura antes da retirada?

  [tex]\qquad \qquad \begin{array}{l c c c}
  mistura: \quad & p & \text{————–} & p-1 \\
  vinho: \quad & p-1 & \text{————–} & V_3 \end{array}[/tex]

  Dessa forma, obtemos que
  [tex]\qquad V_3 \cdot p= \left(p-1\right)\cdot \left(p-1\right)[/tex]
  [tex]\qquad \textcolor{#BC00BC}{\boxed{V_3 = \dfrac{\left(p-1\right)^2}{p}}}[/tex].
  Assim, existe um total de [tex] \dfrac{\left(p-1\right)^2}{p}[/tex] litros de vinho na Mistura 2.
  

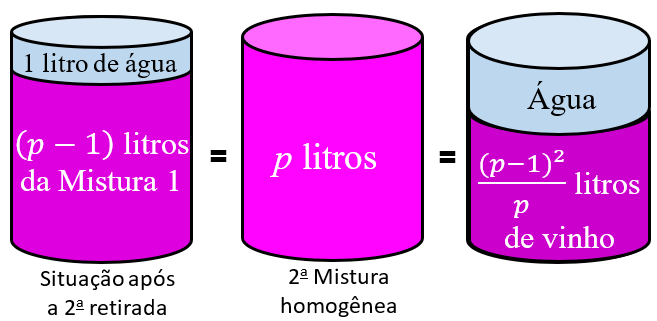
• Vamos repetir o raciocínio anterior, para uma terceira retirada.
  Da segunda mistura homogênea, retirou-se um litro e foi acrescentado um litro de água.
  Vamos utilizar mais uma regra de três simples: se após a retirada de [tex]1[/tex] litro de uma mistura de [tex]p[/tex] litros sobraram [tex]p-1[/tex] litros dessa mistura, qual o correspondente volume [tex]V_4[/tex] que sobrou dos [tex] \dfrac{\left(p-1\right)^2}{p}[/tex] litros de vinho presentes na mistura antes da retirada?

  [tex]\qquad \qquad \begin{array}{l c c c}
  mistura: \quad & p & \text{————–} & p-1 \\
  vinho: \quad & \dfrac{\left(p-1\right)^2}{p} & \text{————–} & V_4 \end{array}[/tex]

  Com isso, obtemos que
  [tex]\qquad V_4 \cdot p= \left(p-1\right)\cdot \dfrac{\left(p-1\right)^2}{p}[/tex]
  [tex]\qquad \textcolor{#BC00BC}{\boxed{V_4 = \dfrac{\left(p-1\right)^3}{p^2}}}[/tex].
  Logo, existe um total de [tex] \dfrac{\left(p-1\right)^3}{p^2}[/tex] litros de vinho na Mistura 3.



• Antes de generalizar o raciocínio que estamos utilizando, vamos repeti-lo mais uma vez, agora para uma quarta retirada.
  Da terceira mistura homogênea, retirou-se um litro e foi acrescentado um litro de água.
  Vamos utilizar outra regra de três simples: se após a retirada de [tex]1[/tex] litro da Mistura 3, de [tex]p[/tex] litros, sobraram [tex]p-1[/tex] litros, qual o correspondente volume [tex]V_5[/tex] que sobrou dos [tex] \dfrac{\left(p-1\right)^3}{p^2}[/tex] litros de vinho contidos na mistura antes da retirada?

  [tex]\qquad \qquad \begin{array}{l c c c}
  mistura: \quad & p & \text{————–} & p-1 \\
  vinho: \quad & \dfrac{\left(p-1\right)^3}{p^2} & \text{————–} & V_5 \end{array}[/tex]

  Dessa forma, obtemos que
  [tex]\qquad V_5 \cdot p= \left(p-1\right)\cdot \dfrac{\left(p-1\right)^3}{p^2}[/tex]
  [tex]\qquad \textcolor{#BC00BC}{\boxed{V_5 = \dfrac{\left(p-1\right)^4}{p^3}}}[/tex].
  Então, existe um total de [tex] \dfrac{\left(p-1\right)^4}{p^3}[/tex] litros de vinho na Mistura 4.
  

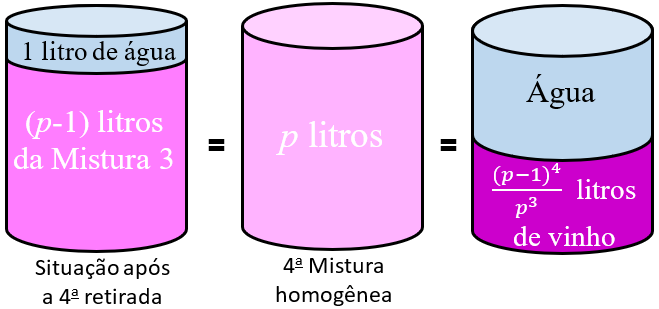
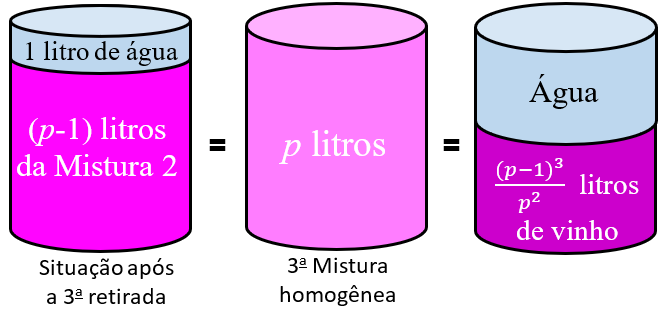
Generalizando o raciocínio e os cálculos, é possível concluir que, após [tex]n[/tex] retiradas, restarão no garrafão [tex]\boxed{V_{n+1} = \dfrac{\left(p-1\right)^n}{p^{n-1}}}[/tex] litros de vinho.

Solução elaborada pelos Moderadores do Blog.