Problema
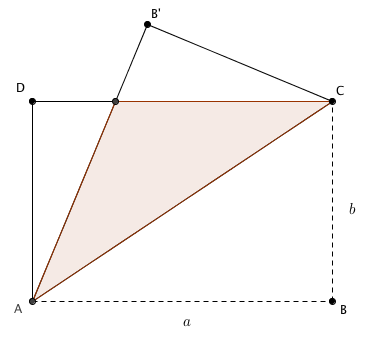
Uma folha retangular com lados medindo [tex]a[/tex] e [tex]b[/tex], sendo [tex]a > b[/tex], foi dobrada ao longo da sua diagonal, conforme mostra a figura abaixo.
Determine, então, a área da região sombreada, em função de [tex]a[/tex] e [tex]b[/tex].
Solução
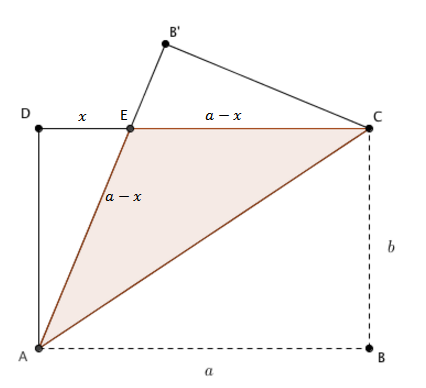
Seja [tex]E[/tex] a interseção entre [tex]\overline{CD}[/tex] e [tex]\overline{AB\,’}[/tex] e considere [tex]DE = x[/tex].
Perceba que [tex]\Delta ADE \equiv \Delta EB\,’C[/tex], pelo caso [tex]LAA_o[/tex]; portanto, temos [tex]AE = EC = DC – DE = a – x[/tex].
Aplicando o teorema de Pitágoras no [tex]\Delta ADE[/tex] obtemos que:
[tex]\qquad \qquad (a – x)^2 = x^2 + b^2[/tex]
[tex]\qquad \qquad \Leftrightarrow a^2 – 2ax + x^2 = x^2 + b^2[/tex]
[tex]\qquad \qquad \Leftrightarrow 2a^2 – 2ax = a^2 + b^2[/tex]
[tex]\qquad \qquad \Leftrightarrow 2a \cdot (a – x) = a^2 + b^2[/tex]
[tex]\qquad \qquad \Leftrightarrow a – x = \dfrac{a^2 + b^2}{2a}[/tex]
Para calcular a área desejada, observe que [tex]\overline{AD}[/tex] é a altura do [tex]\Delta AEC[/tex] relativa a [tex]\overline{CE}[/tex], logo essa área pode ser assim obtida:
[tex]\qquad \qquad Área = \dfrac{(a – x) \cdot b}{2} = \dfrac{b}{2} \cdot \dfrac{a^2 + b^2}{2a} = \dfrac{b \cdot ( a^2 + b^2)}{4a}[/tex].
Solução elaborada pelos Moderadores do Blog.
Nível C – Questão Média
