.Problema de Gincana: Triângulos em um eneágono

Problema

---

Com o objetivo de fazer com que seus alunos fixassem a explicação sobre triângulos isósceles, o Professor Carlos desenhou um eneágono regular no quadro e traçou todas as diagonais do referido polígono.

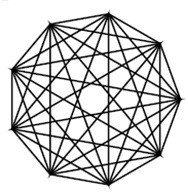
Após concluir o desenho, perguntou aos alunos:
– Quantos triângulos isósceles com os três vértices sobre os vértices desse eneágono existem nessa figura?
Cinco de seus alunos deram as seguintes respostas:

• Alex: Mestre, existem [tex]27[/tex] triângulos;
• Beatriz: Professor, há [tex]36[/tex] triângulos;
• Cibele: Acredito que hajam mais de [tex]50[/tex];
• Diogo: Creio eu que menos de [tex]25[/tex];
• Érica: Com certeza existem [tex]30[/tex] triângulos.

De quem foi a resposta correta?

Solução

---

Nas figuras abaixo, vemos os possíveis tipos de triângulos isósceles com os três vértices sobre os vértices do eneágono que podemos encontrar.

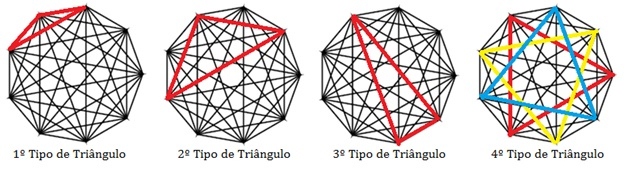
Para cada tipo, podemos contar as seguintes quantidades:
[tex]1^\circ[/tex] tipo: [tex]9[/tex] triângulos;
[tex]2^\circ[/tex] tipo: [tex]9[/tex] triângulos;
[tex]3^\circ[/tex] tipo: [tex]9[/tex] triângulos;
[tex]4^\circ[/tex] tipo: [tex]3[/tex] triângulos.
Deste modo, a quantidade total de triângulos isósceles que há desenhados no eneágono é [tex]30[/tex] e Érica foi quem deu a resposta correta.

---

Solução elaborada pelos Moderadores do Blog.