Problema
Qual é o menor número inteiro que é maior do que o perímetro de qualquer triângulo que possua um lado de tamanho [tex]5 \, [/tex]cm e outro de tamanho [tex]19 \, [/tex]cm?
Solução
Suponha que o terceiro lado de um triângulo que satisfaça as condições do problema seja [tex]x[/tex].
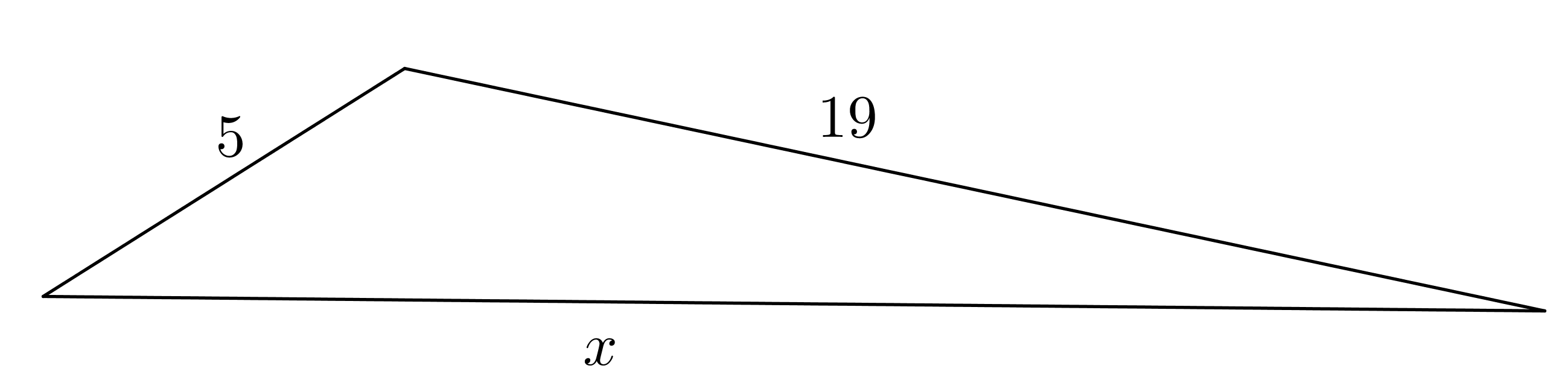
Assim, da desigualdade triangular, temos que
[tex]\qquad x\lt 5+19=24[/tex].
Somando [tex]5+19[/tex] a ambos os lados da desigualdade, ficamos com
[tex]\qquad x+5+19\lt 48[/tex].
Como [tex]x+5+19[/tex] é o perímetro do triângulo em questão, então [tex]48[/tex] é a nossa resposta.
Solução elaborada pelos Moderadores do Blog.
Um aplicativo para ajudar…
Aguarde o aplicativo carregar completamente.
No aplicativo você visualizará um triângulo [tex]ABC[/tex] que possui dois lados com comprimentos fixos: [tex]5 \, [/tex] e [tex] \, 19[/tex] unidades de comprimento. Ao movimentar o ponto [tex]B[/tex] você obterá diversos valores para o terceiro lado.
Assim, movimente o ponto [tex]B[/tex] e verifique que, independente da medida do lado [tex]\overline{BC}[/tex], o perímetro do triângulo será sempre menor do que [tex]48[/tex] unidades de comprimento.
OBMEP_ SRDG, criado com o GeoGebra
Observações:
1) Para movimentar o ponto [tex]B[/tex], basta clicar sobre ele e, mantendo o mouse pressionado, movimentá-lo.
2) Para voltar aos valores inicialmente definidos, clique nas setinhas que aparecem no canto superior direito do applet.
3) Lembre-se de que o GeoGebra fornece valores aproximados para as medidas apresentadas.
Primeira Gincana de 2016 – Clubes de Matemática da OBMEP
Nível A – Questão Média
Nível A – Questão Média