Problema
Dois círculos de raios 2 e 3 são tangentes externos e estão circunscritos a um terceiro círculo, como mostra a figura abaixo.
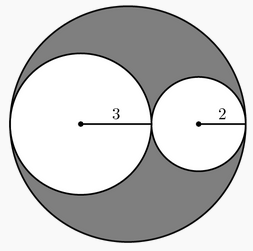
Sabendo-se que os centros desses três círculos são colineares, determine a razão entre a soma das áreas dos círculos menores e a região em cinza.
Solução
Observe que:
- A soma das áreas dos dois círculos internos é:
[tex]\qquad\qquad 3^2\pi + 2^2\pi = (9+4)\pi =13 \pi[/tex]. - A área da região cinza é a área da circunferência maior, que tem raio 5, subtraída a soma das áreas dos círculos menores ([tex]13 \pi[/tex]).
Assim, a área em cinza é
[tex]\qquad\qquad 5^2 \pi – 13 \pi =(25-13)\pi= 12 \pi[/tex],
e, portanto, a razão procurada é [tex] \boxed{\frac{13}{12}_{~_~}} [/tex].
Solução elaborada pelos Moderadores do Blog.
Segunda Gincana de 2015 – Clubes de Matemática da OBMEP
Nível A – Questão Difícil
Nível A – Questão Difícil
