.Problema de Gincana: O que muda?

Problema

---

Na figura, os pontos [tex]M[/tex] e [tex]N[/tex] são, respectivamente, os pontos médios dos lados [tex]PA \, [/tex] e[tex] \, PB[/tex] do triângulo [tex]PAB[/tex].

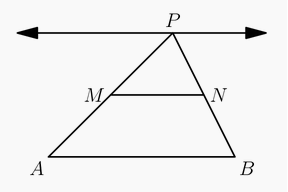
Ao deslizarmos [tex]P[/tex] por uma reta paralela ao lado [tex]AB[/tex], quais das quatro grandezas indicadas a seguir mudarão?

• o comprimento do segmento [tex]MN[/tex];
• o perímetro do triângulo [tex]PAB[/tex];
• a área do triângulo [tex]PAB[/tex];
• a área do trapézio [tex]ABNM[/tex].

Solução

---

(a) Como a medida do lado [tex]AB[/tex] não é alterada e o comprimento do segmento [tex]MN[/tex] é metade do comprimento de [tex]AB[/tex], então [tex]MN[/tex] também não tem sua medida alterada.
(b) Obviamente o perímetro muda, pois as medidas dos segmentos [tex]PA \, [/tex] e[tex] \, PB[/tex] vão mudar, considerando que [tex]P[/tex] ficará “mais longe” ou “mais perto” dos pontos [tex]A[/tex] e [tex]B[/tex].
(c) A área do triângulo [tex]PAB[/tex] não é alterada uma vez que as medidas da base [tex]AB[/tex] e da respectiva altura serão mantidas.
(d) As bases [tex]AB[/tex] e [tex]MN[/tex] do trapézio [tex]ABNM[/tex] não mudam, bem como a sua altura, já que esta é a metade da constante altura do triângulo [tex]ABC[/tex]. Portanto a área do trapézio continua a mesma.
Pelo exposto, apenas uma das grandezas indicadas é alterada: o perímetro do triângulo [tex]PAB[/tex].

---

Solução elaborada pelos Moderadores do Blog.

Simulação

---

Você pode utilizar o applet abaixo para fazer várias simulações do problema.
Basta movimentar o ponto [tex]P[/tex] e verificar as mudanças das várias grandezas envolvidas.