Problema
Na figura, temos os pontos [tex]A = (0 , 9)[/tex], [tex]B = (9 , 9)[/tex], [tex]C = (9 , 0)[/tex], [tex]D = (0 , 0)[/tex] e os pontos [tex]P[/tex] e [tex]Q[/tex] dividem [tex]\overline{DC}[/tex] em três segmentos congruentes.
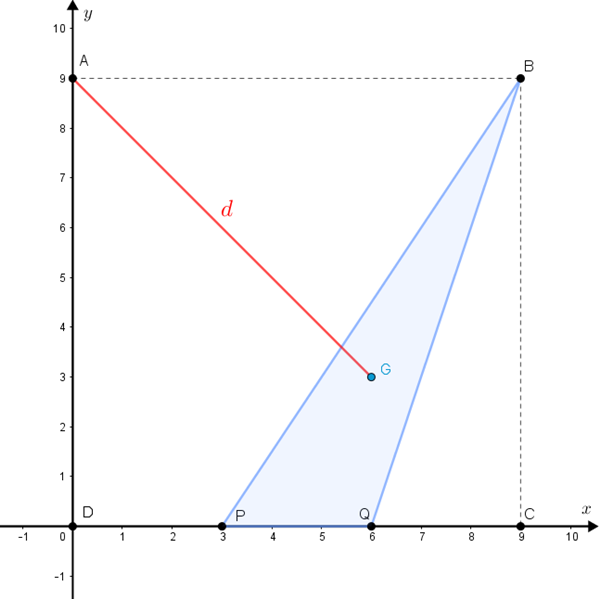
Sabendo que [tex]G[/tex] é o baricentro do triângulo [tex]BPQ[/tex], determine a distância [tex]d[/tex] entre os pontos [tex]A[/tex] e [tex]G[/tex].
Solução
Sendo [tex]B = (9 , 9)[/tex], [tex]P = (3 , 0)[/tex], [tex]Q = (6 , 0)[/tex] e [tex]G = (x, y)[/tex] o baricentro do triângulo [tex]PBQ[/tex], temos
[tex]\qquad x = \dfrac{9 + 3 + 6}{3} = 6 \qquad [/tex] e [tex]\qquad y = \dfrac{0 + 0 + 9}{3} = 3[/tex].
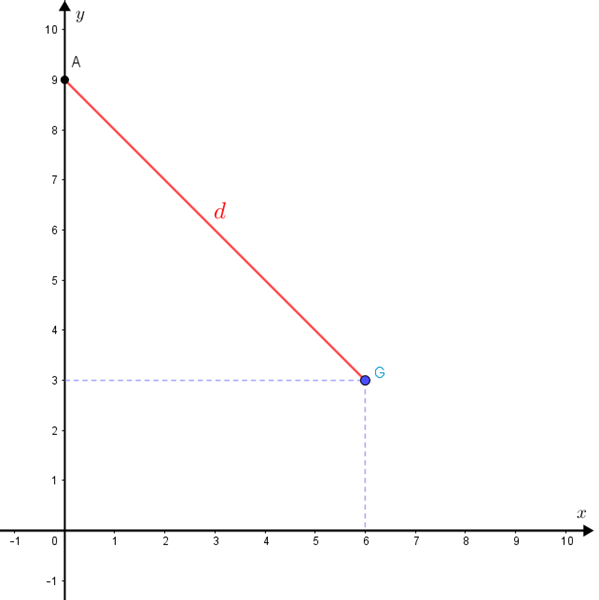
A partir desses dados, podemos calcular a distância [tex]d[/tex] usando as coordenadas dos pontos [tex]A = (0 , 9)\,[/tex] e [tex]\,G = (6 , 3)[/tex]. Vejamos:
[tex]\qquad d = \sqrt{(0-6)^2 + (9-3)^{2^\textcolor{white}{1}}} = 6\sqrt{2^\textcolor{white}{(}}[/tex].
Solução elaborada pelos Moderadores do Blog.
Primeira Gincana de 2015 – Clubes de Matemática da OBMEP
Nível B – Questão Média
Nível B – Questão Média
