✏ Link do problema para dispositivos da Apple.
Problema
Foi feita uma pesquisa em uma escola para determinar a quantidade de estudantes aprovados ou não em matemática e português.
Ao ordenar os nomes dos estudantes em ordem alfabética, o diretor percebeu que 350 estudantes tinham nomes começando com A ou com B. Ao analisar os dados desses 350 estudantes, constatou-se que:
- (i) 70 dos estudantes cujos nomes começam com B foram aprovados em matemática.
(ii) 60 dos estudantes cujos nomes começam com B foram aprovados em português.
(iii) 80 estudantes cujos nomes começam com A e 50 estudantes cujos nomes começam com B não foram aprovados em nenhuma das duas disciplinas.
(iv) Exatamente 160 estudantes têm nomes que começam com B.
(v) Dos estudantes cujos nomes começam com A ou com B, 50 foram aprovados nas duas disciplinas.
(vi) Dos estudantes cujos nomes começam com A ou com B, 110 foram aprovados somente em matemática.
Quantos alunos cujos nomes começam com A foram aprovados apenas em português?
(Adaptado da II ONEM.)
Solução
Vamos utilizar o esquema gráfico abaixo, para registrar os dados convenientemente. Nesse esquema, a parte superior representa os estudantes cujos nomes começam com A e, a parte inferior, os estudantes cujos nomes começam com B.
Se denotarmos por [tex]a[/tex] o número de alunos cujos nomes começam com A que foram aprovados apenas em português, como [tex]80[/tex] estudantes cujos nomes começam com A e [tex]50[/tex] estudantes cujos nomes começam com B não foram aprovados em nenhuma das duas disciplinas ((iii)), podemos fazer um primeiro registro dos dados:
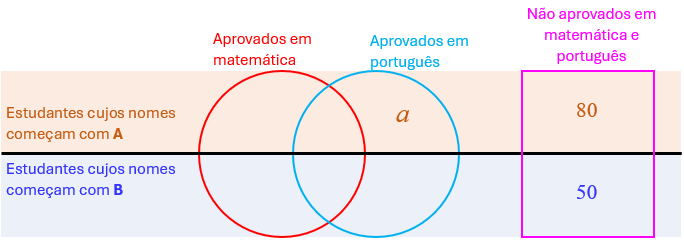
Sabemos que dentre os [tex]160[/tex] estudantes cujos nomes começam com B ((iv)), [tex]50[/tex] não foram aprovados em nenhuma das duas disciplinas; assim, [tex]\boxed{160-50=110}[/tex] estudantes cujos nomes começam com B foram aprovados em uma ou nas duas disciplinas.
Mas também sabemos que, dentre os estudantes cujos nomes começam com B, [tex]70[/tex] foram aprovados em matemática ((i)) e [tex]60[/tex] foram aprovados em português ((ii)); com isso, podemos concluir que [tex]\boxed{(70+60)-110=\textcolor{blue}{20}}[/tex] estudantes cujos nomes começam com B foram aprovados nas duas disciplinas.
Com isso, desses estudantes, [tex]\boxed{70-20=\textcolor{blue}{50}}[/tex] foram aprovados apenas em matemática e [tex]\boxed{60-20=\textcolor{blue}{40}}[/tex] foram aprovados apenas em português, e já podemos fazer um segundo registro.
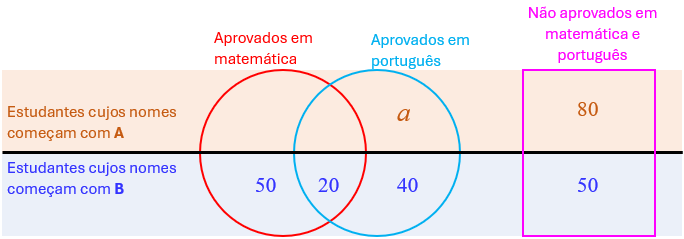
Os dados do problema indicam que [tex]50[/tex] dos estudantes cujos nomes começam com A ou com B foram aprovados nas duas disciplinas ((v)). Como já sabemos que, dentre aqueles cujos nomes começam com B, [tex] 20[/tex] foram aprovados nas duas disciplinas, então [tex]\boxed{50-20=\textcolor{#ED8137}{30}}[/tex] estudantes cujos nomes começam com A foram aprovados nas duas disciplinas.
Vejam o novo esquema:
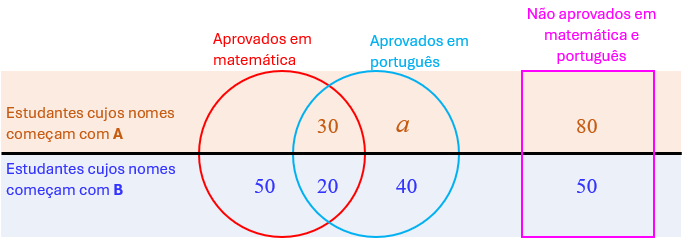
O último dado do problema nos informa que, dos estudantes cujos nomes começam com A ou com B, [tex]110[/tex] foram aprovados somente em matemática ((vi)); mas sabemos que, dentre esses estudantes, [tex]50[/tex] têm o nome começando por B; então [tex]\boxed{110-50=\textcolor{#ED8137}{60}}[/tex] estudantes cujos nomes começam com A foram aprovados somente em matemática.
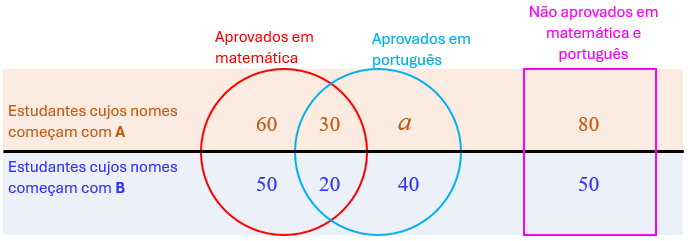
Para finalizar, observe que pelo esquema o total de estudantes pesquisados que tinham nomes começando com A ou com B é dado pela soma [tex]\textcolor{#ED8137}{60+30+a+80}+\textcolor{blue}{50+20+40+50}[/tex]; mas o enunciado do problema garante que esse total é 350. Dessa forma, segue que:
[tex]\qquad \textcolor{#ED8137}{60+30+a+80}+\textcolor{blue}{50+20+40+50}=350\\
\qquad \textcolor{#ED8137}{170+a}+\textcolor{blue}{160}=350\\
\qquad \textcolor{#ED8137}{a}=350-\textcolor{blue}{160}-\textcolor{#ED8137}{170}\\
\qquad \textcolor{#ED8137}{a}=350-\textcolor{blue}{160}-\textcolor{#ED8137}{170}\\
\qquad \textcolor{#ED8137}{a=20}.\\
[/tex]
Portanto, o número de alunos cujos nomes começam com A aprovados apenas em português é [tex] \fcolorbox{black}{#FAD9C3}{$20$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Difícil
Nível A – Questão Difícil
