✏ Link do problema para dispositivos da Apple.
Problema
Observe a figura abaixo.
- A distância do topo do cubo no chão até o topo do cilindro na mesa é de [tex]1\,\text{m}.[/tex]
- A distância do topo do mesmo cilindro no chão até o topo do mesmo cubo na mesma mesa é de [tex]\dfrac{4}{5}\,\text{m}[/tex].
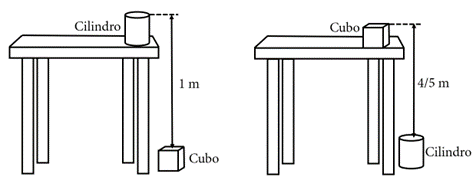
Encontre a altura da mesa. Dê sua resposta em metros.
Solução
Vamos denotar por [tex]x[/tex] a altura do cilindro e por [tex]y[/tex] a altura do cubo. Com isso, vamos atualizar as medidas que aparecem na figura original do problema:
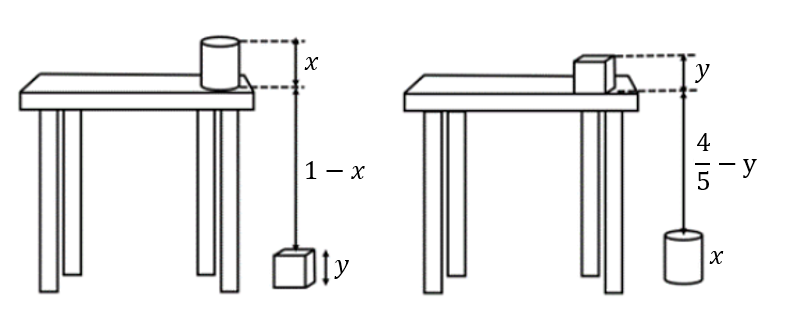
Observe que temos duas expressões para a altura da mesa: [tex]\boxed{1-x+y}~[/tex] e [tex]~\boxed{\dfrac{4}{5}-y+x}[/tex]; assim, segue que:
[tex]\qquad 1-x+y=\dfrac{4}{5}-y+x \\
\qquad 2x-2y=\dfrac{1}{5}\\
\qquad x-y=\dfrac{1}{10}.[/tex]
Portanto, a altura da mesa pode ser assim calculada:
[tex]\qquad \textcolor{blue}{altura}=1-x+y=1-(x-y)\\
\qquad \textcolor{blue}{altura}=1-\dfrac{1}{10}\\
\qquad \textcolor{blue}{\boxed{altura=\dfrac{9}{10}\ \text{m}}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Mediana
Nível A – Questão Mediana
