Problema
(Indicado a partir do 1º ano do E. M.)
A figura seguinte mostra um triângulo retângulo [tex]ABC[/tex]. O ponto [tex]M[/tex] é o ponto médio do lado [tex]\overline{AB}[/tex], que é a hipotenusa.
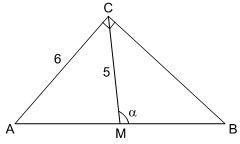
Calcule o valor de [tex]\cos\alpha[/tex].
Extraído de UNICAMP.

Lembretes
[tex]\textcolor{#800000}{\textbf{(i)}}\; \textbf{ (Lei dos Cossenos)}[/tex] Em um triângulo [tex]ABC[/tex] qualquer, para lados opostos aos ângulos internos [tex]{\displaystyle {\widehat {A}},{\widehat {B}}}[/tex] e [tex]{\displaystyle {\widehat {C}},} [/tex] com medidas respectivamente [tex]{\displaystyle a,b}[/tex] e [tex]{\displaystyle c,}[/tex] valem as relações:
[tex]\quad {\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos{\widehat {A}}\,\!}[/tex];
[tex]\quad {\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos{\widehat {B}}\,\!}[/tex];
[tex]\quad {\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos{\widehat {C}}\,\!}[/tex].
[tex]\textcolor{#800000}{\textbf{(ii)}}\;[/tex] A mediana de um triângulo retângulo relativa à hipotenusa mede metade da hipotenusa.
Solução
Como [tex]M[/tex] é o ponto médio da hipotenusa do triângulo [tex]ABC[/tex], [tex]\overline{CM}[/tex] é a mediana do triângulo retângulo relativa à hipotenusa. Dessa forma, temos que [tex]AM = MB = CM = 5[/tex].
Pelo teorema de Pitágoras no triângulo [tex]ABC[/tex]:
[tex]\qquad AC^{2}+CB^{2}=AB^{2}[/tex]
[tex]\qquad 6^2+CB^{2}=10^2[/tex]
[tex]\qquad CB=8[/tex].
Aplicando a lei dos cossenos no triângulo [tex]BMC[/tex], obtemos:
[tex]\qquad BC^2=CM^2+MB^2-2 \cdot CM \cdot MB \cdot \cos \alpha[/tex]
[tex]\qquad 8^2=5^2+5^2-2 \cdot5 \cdot 5 \cdot \cos \alpha[/tex]
[tex]\qquad 64=25+25-50 \cdot \cos \alpha[/tex]
[tex]\qquad \cos\alpha = \dfrac{-7}{25}[/tex].
Solução elaborada pelos Moderadores do Blog.
