Problema
(Indicado a partir do 7º ano do E. F.)
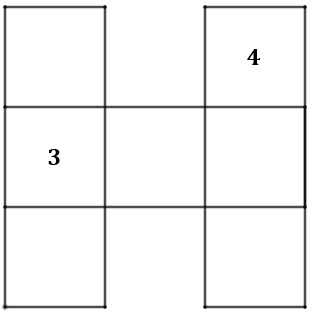
Na figura, vemos três fileiras de três quadrados: uma horizontal e duas verticais.
É possível escrever os números de [tex]1[/tex] a [tex]7[/tex], um em cada quadrado, de modo que a soma dos três números em cada uma das três fileiras seja a mesma? Já foram colocados os números [tex]3[/tex] e [tex]4[/tex].
Solução
Chamemos de [tex]x[/tex] o número que ficará exatamente no quadrado abaixo do número [tex]4[/tex].
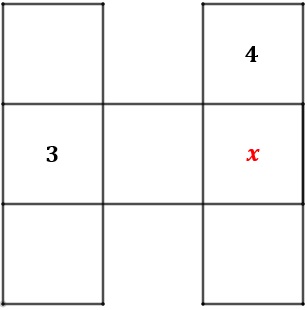
Seja [tex]S[/tex] a soma dos elementos em cada uma das três fileiras. Somando todos os elementos das três fileiras, os números [tex]3[/tex] e [tex]x[/tex] serão somados duas vezes, e, os demais, apenas uma. Dessa forma:
[tex]\qquad 3 \cdot S=1+2+3+4+5+6+7+3+x[/tex]
[tex]\qquad 3 \cdot S=31+x[/tex] .
Como [tex]3 \cdot S[/tex] é um número inteiro (pois [tex]S[/tex] é inteiro), [tex]31+x[/tex] deve ser um número divisível por [tex]3[/tex].
Pelo enunciado, os números disponíveis para [tex]x[/tex] são [tex]1[/tex], [tex]2[/tex], [tex]5[/tex], [tex]6[/tex] ou [tex]7[/tex]; mas os únicos que tornam [tex]31+x[/tex] divisível por [tex]3[/tex] são [tex]x=2[/tex] e [tex]x=5[/tex]. Vamos analisar separadamente as duas possibilidades.
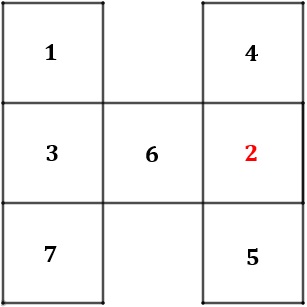
- Caso [tex]x=2[/tex], teremos [tex]S=11[/tex]. Daí, podemos completar a figura da seguinte forma:
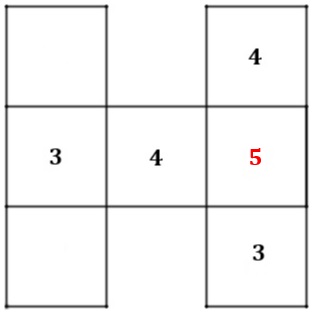
- Caso [tex]x=5[/tex], teremos [tex]S=12[/tex]. Ao tentarmos completar a figura, chegamos a uma situação com repetição de números.
Observe que, para que a soma em cada linha resulte em [tex]12[/tex], devemos, no mínimo, repetir os valores [tex]3[/tex] e [tex]4[/tex]. O que é impossível pelo enunciado.
Portanto, a única solução possível é a primeira.
Solução elaborada pelos Moderadores do Blog.
