Problema
(Indicado a partir do 8º ano do E. F.)
Um avião regressa dos jogos olímpicos transportando os cinco primeiros classificados numa determinada competição em que não houve dois na mesma colocação. Eles afirmam:
- Atleta A – Eu não fui o quinto colocado.
- Atleta B – C foi o terceiro colocado.
- Atleta C – A ficou pior colocado do que E.
- Atleta D – E foi o segundo colocado.
- Atleta E – D não foi o quinto colocado.
Sabendo que apenas o primeiro e o segundo colocados mentiram, quais os resultados possíveis dessa competição?
Solução 1
(1) Suponha que E não tenha sido o segundo colocado.
Então, D mentiu e, portanto, ele foi um dos dois primeiros. Assim, E falou a verdade, não podendo ter sido um dos dois primeiros colocados.
[tex]\qquad \qquad \begin{array}{cc}
&? \, \, \, \, \, \, ?& ?\quad ?\quad?\\
&{\underbrace{\overline{1^{\circ}} \, \, \overline{2^{\circ}}}_{D}}& {\underbrace{\overline{3^{\circ}} \, \, \overline{4^{\circ}} \, \, \overline{5^{\circ}}}_{E}}
\end{array}[/tex]
(1.1) Suponha que B tenha falado a verdade.
Neste caso, C foi o terceiro e, portanto, C falou a verdade, logo E foi o quarto e A o quinto.
[tex]\qquad \qquad \begin{array}{cccc}
& \, &C&E&A\\
&{\underbrace{\overline{1^{\circ}}\quad\overline{2^{\circ}}}_{D}}& \overline{3^{\circ}}&\overline{4^{\circ}} &\overline{5^{\circ}}
\end{array}[/tex]
Absurdo; pois, sendo o quinto colocado, a afirmação de A seria falsa e A não mentiu, pois apenas os dois primeiros colocados mentem. Assim B não falou a verdade.
(1.2) Como B mentiu, ele também foi um dos dois primeiros, cabendo a A, E e C as últimas colocações entre os cinco e sendo suas afirmações verdadeiras.
[tex]\qquad \qquad \begin{array}{cc}
&? \, \, \, \, \, \, ?& ?\quad ?\quad?\\
&{\underbrace{\overline{1^{\circ}} \, \, \overline{2^{\circ}}}_{B, \, D}}& {\underbrace{\overline{3^{\circ}} \, \, \overline{4^{\circ}} \, \, \overline{5^{\circ}}}_{A, \, C,E}}
\end{array}[/tex]
Como C falou a verdade, temos E em terceiro e A em quarto, restando o quinto lugar para C.
[tex]\qquad \qquad \begin{array}{cccc}
&? \, \, \, \, \, \, ?& E & A & C\\
&{\underbrace{\overline{1^{\circ}} \, \, \overline{2^{\circ}}}_{B, \, D}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}[/tex]
Dessa forma, são classificações possíveis:
[tex]\quad \boxed{\begin{array}{ccccc}
&D & B & E & A & C\\
&\overline{1^{\circ}}&\overline{2^{\circ}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}\quad} \quad[/tex] e [tex]\quad \boxed{\begin{array}{ccccc}
&B & D & E & A & C\\
&\overline{1^{\circ}}&\overline{2^{\circ}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}\quad}[/tex]
(2) Suponha, agora, que E tenha sido realmente o segundo colocado.
Então, E mentiu na afirmação e, portanto, D foi o quinto colocado.
[tex]\quad \qquad \begin{array}{ccccc}
&? & E & ?& ? & D\\
&\overline{1^{\circ}}&\overline{2^{\circ}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}[/tex]
(2.1) Caso B tenha falado a verdade, C terá sido o terceiro e B o quarto.
[tex]\quad \qquad \begin{array}{ccccc}
&? & E & C & B & D\\
&\overline{1^{\circ}}&\overline{2^{\circ}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}[/tex]
Mas restaria apenas o primeiro lugar para A, fazendo com que a afirmação de C seja falsa, o que é um absurdo, pois apenas os dois primeiros colocados mentiram. Assim, B não pode ter falado a verdade.
(2.2) Como B mentiu, então B terá sido o primeiro e C o quarto, restando assim o terceiro lugar para A.
Dessa forma, outro resultado possível será
[tex]\qquad \qquad \boxed{\begin{array}{ccccc}
&B & E & A & C & D\\
&\overline{1^{\circ}}&\overline{2^{\circ}}& \overline{3^{\circ}}&\overline{4^{\circ}}&\overline{5^{\circ}}
\end{array}\quad}. [/tex]
➤ Pelo exposto, há três possíveis resultados da competição em questão:
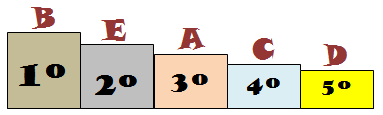 |
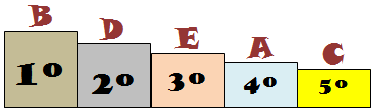 |
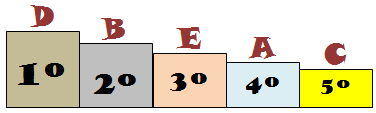 |
Solução elaborada pelos Moderadores do Blog.
Solução 2
Em qualquer caso deve haver sempre [tex]2[/tex] mentirosos. Assim, podemos listar todas as duplas de possíveis mentirosos:
[tex]\qquad – \, A[/tex] e [tex]B[/tex]
[tex]\qquad – \, A[/tex] e [tex]C[/tex]
[tex]\qquad – \, A[/tex] e [tex]D[/tex]
[tex]\qquad – \, A[/tex] e [tex]E[/tex]
[tex]\qquad – \, B[/tex] e [tex]C[/tex]
[tex]\qquad – \, B[/tex] e [tex]D[/tex]
[tex]\qquad – \, B[/tex] e [tex]E[/tex]
[tex]\qquad – \, C[/tex] e [tex]D[/tex]
[tex]\qquad – \, C[/tex] e [tex]E[/tex]
[tex]\qquad – \, D[/tex] e [tex]E[/tex]
dando [tex]10[/tex] no total. Mas, antes de analisar todas elas, vamos observar algumas coisas:
- O competidor [tex]A[/tex] diz: Eu não fui o quinto colocado.
Supondo que ele minta, logo ele será o quinto colocado, o que seria um absurdo pois quem mente deve ficar ou em [tex]1^\circ[/tex] ou em [tex]2^\circ[/tex] lugar. Logo, é impossível [tex]A[/tex] mentir. Isso ainda nos mostra que [tex]A[/tex] só pode ficar em [tex]3^\circ[/tex] ou em [tex]4^\circ[/tex] lugar, pois ele afirma não estar em [tex]5^\circ[/tex] lugar, além disso fala a verdade, ou seja, não está em [tex]1^\circ[/tex] ou [tex]2^\circ[/tex] lugar.
Assim, já podemos eliminar [tex]4[/tex] casos: [tex]A[/tex] e [tex]B[/tex], [tex]A[/tex] e [tex]C[/tex], [tex]A[/tex] e [tex]D[/tex] e [tex]A[/tex] e [tex]E[/tex]. - Agora vamos focar no competidor [tex]C[/tex]: para [tex]C[/tex] mentir, [tex]D[/tex] deve obrigatoriamente mentir também. Isso porque [tex]C[/tex] diz que [tex]A[/tex] ficou mais mal colocado que [tex]E[/tex], mas, se ele mentir, isso quer dizer que [tex]A[/tex] ficou numa posição acima de [tex]E[/tex]. Como [tex]A[/tex] só pode ficar em [tex]3^\circ[/tex] ou em [tex]4^\circ[/tex], logo [tex]E[/tex] teria que ficar obrigatoriamente em [tex]4^\circ[/tex] ou em [tex]5^\circ[/tex]. Mas [tex]D[/tex] diz que [tex]E[/tex] ficaria na [tex]2^\circ[/tex] colocação; logo, para [tex]C[/tex] mentir, [tex]D[/tex] também deve mentir.
Mas perceba que, se os dois mentirem, [tex]B[/tex] estará falando a verdade e [tex]B[/tex] diz: [tex]C[/tex] foi o terceiro colocado. Acontece que se [tex]C[/tex] mente, ele deve ser o [tex]1^\circ[/tex] ou o [tex]2^\circ[/tex] colocado, assim podemos ver que é impossível [tex]C[/tex] mentir.
Desse modo, podemos eliminar mais três casos: [tex]B[/tex] e [tex]C[/tex], [tex]C[/tex] e [tex]D[/tex] e [tex]C[/tex] e [tex]E[/tex].
Com isso, restaram apenas [tex]3[/tex] casos. Vamos analisar um por um:
-
(i) [tex]B[/tex] e [tex]D[/tex]
Se [tex]A[/tex] ficou mais mal colocado que [tex]E[/tex] como diz [tex]C[/tex], logo, [tex]E[/tex] deve ficar na [tex]3^\circ[/tex] colocação e [tex]A[/tex] na [tex]4^\circ[/tex], já que [tex]A[/tex] só pode ficar na [tex]3^\circ[/tex] ou na [tex]4^\circ[/tex] colocação e [tex]E[/tex] diz a verdade, ou seja, não ficou em [tex]1^\circ[/tex] ou [tex]2^\circ[/tex] lugar. Assim, resta para [tex]C[/tex] a [tex]5^\circ[/tex] colocação, ficando indefinido em qual colocação [tex]B[/tex] e [tex]D[/tex] ficariam.
[tex]\qquad 1. \, B[/tex] ou [tex]D[/tex]
[tex]\qquad 2. \, D[/tex] ou [tex]B[/tex]
[tex]\qquad 3. \, E[/tex]
[tex]\qquad 4. \, A[/tex]
[tex]\qquad 5. \, C[/tex]
Desse modo podemos concluir que, se [tex]B[/tex] e [tex]D[/tex] mentirem, há duas possibilidades.
- (ii) [tex]B[/tex] e [tex]E[/tex]
Se [tex]E[/tex] que diz que [tex]D[/tex] não foi o quinto colocado está mentindo, logo [tex]D[/tex] foi o quinto colocado. Além disso, [tex]D[/tex], que diz a verdade, fala que [tex]E[/tex] ficou na segunda colocação, assim [tex]B[/tex] obrigatoriamente deve ficar na primeira. [tex]B[/tex], que está mentindo, diz que [tex]C[/tex] ficou em terceiro, sendo assim podemos concluir que ele ficou em quarto, restando para [tex]A[/tex] a terceira colocação.
[tex]\qquad 1. \, B[/tex]
[tex]\qquad 2. \, E[/tex]
[tex]\qquad 3. \, A[/tex]
[tex]\qquad 4. \, C[/tex]
[tex]\qquad 5. \, D[/tex]
Assim, se [tex]B[/tex] e [tex]E[/tex] mentirem, teremos uma possibilidade.
- (iii) [tex]D[/tex] e [tex]E[/tex]
Aqui, devemos observar que o competidor [tex]E[/tex] diz: [tex]D[/tex] não foi o quinto colocado. Mas [tex]E[/tex] está mentindo, logo [tex]D[/tex] foi o quinto colocado, o que não é possível pois [tex]D[/tex] é mentiroso, devendo ficar na primeira ou na segunda posição.
Assim, é impossível [tex]D[/tex] e [tex]E[/tex] mentirem ao mesmo tempo.
Com isso, podemos ver que há no total [tex]3[/tex] possibilidades de resultado:
| [tex]1. \, B[/tex] [tex]2. \, D[/tex] [tex]3. \, E[/tex] [tex]4. \, A[/tex] [tex]5. \, C[/tex] |
[tex]1. \, D[/tex] [tex]2. \, B[/tex] [tex]3. \, E[/tex] [tex]4. \, A[/tex] [tex]5. \, C[/tex] |
[tex]1. \, B[/tex] [tex]2. \, E[/tex] [tex]3. \, A[/tex] [tex]4. \, C[/tex] [tex]5. \, D[/tex] |
Solução elaborada pelo COM 1uik.
