Problema
(Indicado a partir do 2º ano do E. M.)
No desenho abaixo, três dos quadrados menores deverão ser pintados de verde, três de amarelo e três de azul.
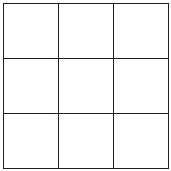
Se os quadrados da linha horizontal do meio tiverem a mesma cor, qual o número de formas diferentes de se colorir o desenho?
Solução 1
Temos que pintar três quadradinhos de verde, três de azul e três de amarelo: no total temos [tex]9[/tex] quadradinhos.
- Considerando que temos [tex]9[/tex] cores, sendo três a três repetidas, teremos [tex]9[/tex] maneiras de pintar o primeiro quadradinho da linha do meio; para o segundo da linha do meio temos [tex]2[/tex] maneiras, já que ele deve ser da mesma cor do outro; para o terceiro da linha do meio [tex]1[/tex] maneira, totalizando, então, [tex]9\cdot2\cdot1=18[/tex] maneiras.
- Sobram [tex]6[/tex] quadradinhos e [tex]6[/tex] cores; assim, teremos [tex]6![/tex] maneiras de colori-los.
- Como temos que pintar os quadradinhos do meio e os outros, multiplicamos: [tex]18\cdot6![/tex]
- Como as cores se repetem três a três, temos:
[tex]\dfrac{18\cdot6!}{3! \, 3! \, 3!}=\dfrac{\cancel{6}\cdot3\cdot\cancel{6}\cdot5\cdot4\cdot\cancel{3!}}{\cancel{3!}\cancel{3!}\cancel{3!}}=5\cdot4\cdot3=60[/tex] formas diferentes de se colorir o desenho.
Solução elaborada pelo COM Parentesco Genial, com contribuições dos Moderadores do Blog.
Solução 2
- Suponha que pintemos a linha horizontal do meio com verde.
Resta pintarmos [tex]6[/tex] quadrados, sendo [tex]3[/tex] com amarelo e [tex]3[/tex] com azul.
- O número de formas de se fazer essa pintura é [tex]P_6^{(3, 3)}=\dfrac{6!}{3!3!}=20[/tex].
Porém, a linha horizontal do meio pode ser pintada com qualquer das [tex]3[/tex] cores.
- Deste modo, o número total de formas de colorirmos o desenho nas condições dadas é [tex]3\cdot 20=60[/tex].
Solução elaborada pelosModeradores do Blog.
Participou da discussão o COM Parentesco Genial.
