Problema
(Indicado a partir do 9º ano do E. F.)
A partir das informações da figura a seguir e sabendo que [tex]\beta+\gamma=270^\circ[/tex], calcule [tex]x[/tex].
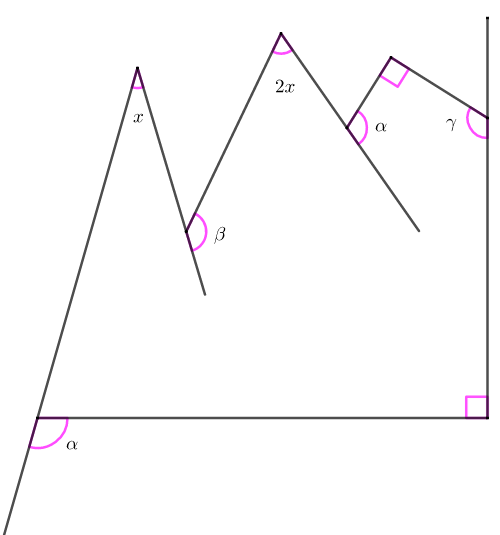
Adaptado de Geometría y Trigonometría – Centro Pre-Universitario de la Universidad Nacional Jorge Basadre Grohmann.

Lembretes
(1) Ângulos opostos pelo vértice possuem a mesma medida.
(2) “Teorema dos Bicos”: Se entre duas retas paralelas traçarmos segmentos formando “bicos” (uma poligonal simples definida por transversais às retas paralelas), a soma das medidas dos ângulos com bicos (vértices) apontando para um lado é igual à soma das medidas dos ângulos com bicos (vértices) apontando para o lado oposto, independentemente da quantidade de tais ângulos.
Solução
Observe que, utilizando os pontos marcados na figura abaixo, temos que [tex]K\hat{A}L=\alpha-90^\circ[/tex]. Assim, pelo Lembrete 1, segue que [tex]\boxed{F\hat{A}D=\alpha-90^\circ}\,.[/tex]
Além disso, nos pontos [tex]G,J[/tex] e [tex]C[/tex] podemos marcar as medidas angulares suplementares, obtendo no total as medidas angulares destacadas na figura abaixo.
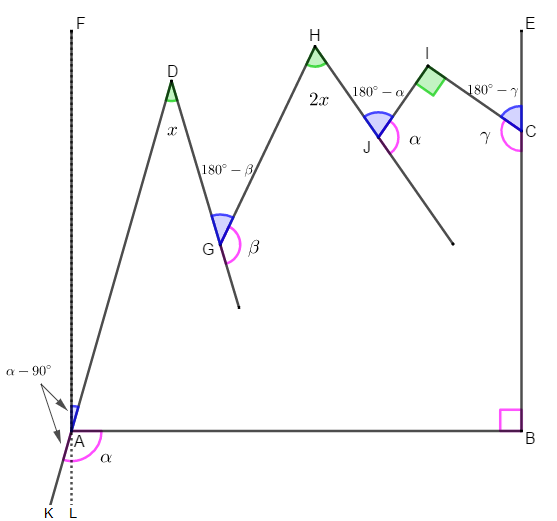
Agora, podemos utilizar o Lembrete 2 (“Teorema dos Bicos”) para obter a próxima equação: vamos igualar a soma das medidas dos ângulos "com bicos para baixo" (ângulos destacados em azul) e a soma das medidas dos ângulos "com bicos para cima" (ângulos destacados em verde):
[tex]\qquad \underbrace{\color{blue}(\alpha-90^\circ)+(180^\circ-\beta)+(180^\circ-\alpha)+(180^\circ-\gamma)\color{black}}_{\text{bicos para baixo}}=\underbrace{\color{#28ce20}x+2x+90^\circ}_{\text{bicos para cima}}.[/tex]
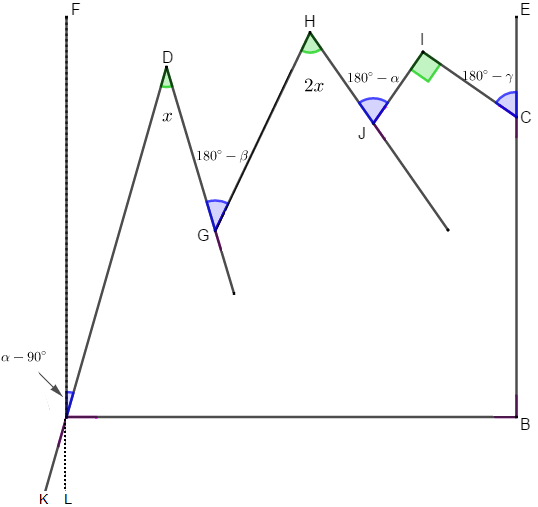
Logo:
[tex]\qquad \cancel{\alpha}-90^\circ+180^\circ-\beta+180^\circ\cancel{-\alpha}+180^\circ-\gamma=3x+90^\circ[/tex]
[tex]\qquad 450^\circ-(\beta+\gamma)=3x+90^\circ.[/tex]
Como, de acordo com as informações do problema, [tex]\beta+\gamma=270^\circ[/tex], segue que:
[tex]\qquad 450^\circ-270^\circ=3x+90^\circ\\
\qquad 180^\circ=3x+90^\circ\\
\qquad 3x=90^\circ\\
\qquad \fcolorbox{black}{#BFFFBF}{$x=30^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Para aprender mais…
Teorema dos Bicos I
Treinamento Olímpico em Matemática oferecido para Estudantes do Oitavo e Nono Anos
do Ensino Fundamental das escolas Públicas e Privadas de Pirassununga-SP e região.
