✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
A soma das áreas dos três quadrados que aparecem na figura é igual a [tex]83 \text{ cm}^2[/tex].
Calcule a área do quadrado maior.
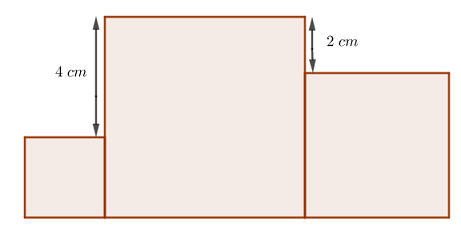
(UFPR, 2010 – 1ª Fase.)
Solução
Considere [tex]x[/tex] e [tex]y[/tex] os comprimentos em centímetros dos lados dos quadrados da esquerda e da direita, respectivamente.
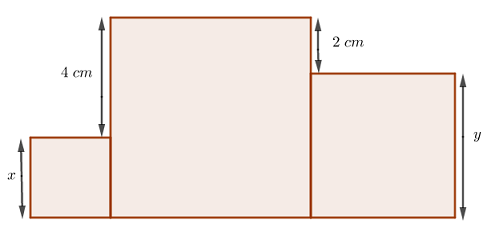
Observe que [tex]y+2=x+4[/tex], ou seja, [tex]\fcolorbox{#800000}{#ffffff}{$y=x+2$}.\;\;\;\;\;\;\;\;\textcolor{#800000}{(i)}[/tex]
Sabemos que a área de um quadrado qualquer é a medida do seu lado elevada ao quadrado; assim, considerando o lado do quadrado maior igual a [tex]x+4[/tex] e a soma das áreas dos três quadrados igual a [tex]83 \text{ cm}^2[/tex], obtemos:
[tex]\qquad x^2+(x+4)^2+y^2=83.[/tex]
Assim, segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad x^2+(x+4)^2+(x+2)^2=83[/tex]
[tex]\qquad x^2+x^2+8x+16+x^2+4x+4=83[/tex]
[tex]\qquad 3x^2+12x+20-83=0[/tex]
[tex]\qquad \boxed{3x^2+12x-63=0}\,.[/tex]
Vamos resolver a equação do [tex]2^{\circ}[/tex] grau obtida para encontrarmos a medida do lado do quadrado menor.
Os coeficientes dessa equação são [tex]a=3[/tex], [tex]b=12[/tex] e [tex]c=-63[/tex]; logo, temos
[tex]\qquad \Delta=b^2-4ac[/tex]
[tex]\qquad \Delta=12^2-4\cdot 3\cdot (-63)[/tex]
[tex]\qquad \Delta=144+756[/tex]
[tex]\qquad \Delta=900[/tex],
donde:
[tex]\qquad x=\dfrac{-b\pm\sqrt{\Delta}}{2a}\\
\qquad x=\dfrac{-12\pm\sqrt{900}}{2\cdot 3}\\
\qquad x=\dfrac{-12\pm30}{6}\\[/tex]
e, assim,
[tex]\qquad x=\dfrac{-12-30}{6}=\dfrac{-42}{6}=-7[/tex]
ou
[tex]\qquad x=\dfrac{-12+30}{6}=\dfrac{18}{6}=3.[/tex]
Como [tex]x[/tex] corresponde ao comprimento do lado do quadrado menor, [tex]x \gt 0[/tex]. Então [tex]x=3\text{ cm}\,.[/tex] Portanto, o lado do quadrado maior é [tex]4+x=4+3=7\text{ cm}[/tex] e, consequentemente, sua área é [tex]\,\fcolorbox{black}{#eee0e5}{$7^2=49\text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
