Problema
(Indicado a partir do 1º ano do E. M.)
(UNIFOR – Adaptada) Um cavalo está preso por uma corda do lado de fora de um galpão retangular fechado de [tex]6[/tex] metros de comprimento por [tex]4[/tex] metros de largura. A corda tem [tex]10[/tex] metros de comprimento e está fixada em uma das quinas das paredes do galpão, na altura do pescoço do cavalo, conforme ilustra a figura.
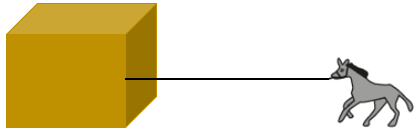
Determine a área total da região máxima na qual o animal pode se deslocar.
Solução
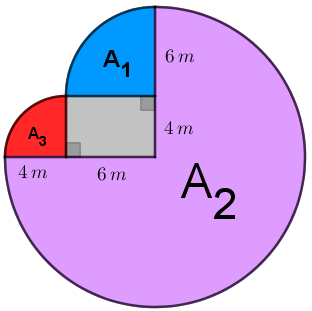
Vamos decompor a região na qual o cavalo pode se deslocar em três partes:
- área [tex]\textcolor{#0099FF}{A_1}[/tex], descrita por [tex]\dfrac{1}{4}[/tex] de um círculo de raio [tex]6 \, m[/tex],
- área [tex]\textcolor{#CC66FF}{A_2}[/tex], descrita por [tex]\dfrac{3}{4}[/tex] de um círculo de raio [tex]10 \, m[/tex],
- área [tex]\textcolor{#FF0000}{A_3}[/tex], descrita por [tex]\dfrac{1}{4}[/tex] de um círculo de raio [tex]4 \, m[/tex],
conforme mostra a figura abaixo.
Calculemos, então, a medida da área total da região em questão adicionando as medidas das áreas dos setores circulares [tex]\textcolor{#0099FF}{A_1}[/tex], [tex]\textcolor{#CC66FF}{A_2}[/tex] e [tex]\textcolor{#FF0000}{A_3}[/tex]:
[tex]\qquad A=\textcolor{#0099FF}{A_1}+\textcolor{#CC66FF}{A_2}+\textcolor{#FF0000}{A_3}\\
\qquad A=\textcolor{#0099FF}{\dfrac{1}{4}\cdot \pi \cdot 6^2}+\textcolor{#CC66FF}{\dfrac{3}{4}\cdot \pi \cdot 10^2}+ \textcolor{#FF0000}{\dfrac{1}{4}\cdot \pi \cdot 4^2}\\
\qquad A=88\pi \, m^2.[/tex]
Assim, a medida da área total da região máxima na qual o animal pode se deslocar é [tex] \, \fcolorbox{black}{#eee0e5}{$88\pi \, m^2$} \, [/tex], aproximadamente, [tex] \, \fcolorbox{black}{#eee0e5}{$276\ m^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
