✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1ª série do E. M.)
Um jogo apresenta, em parte da tela, um radar térmico que, na cor cinza, indica a região de uma floresta em chamas. Nesse radar, as circunferências são concêntricas em [tex]O[/tex] e as medidas de seus raios estão indicadas na imagem. Há também seis retas que passam pelo ponto [tex]O[/tex] e dividem as circunferências em arcos de mesma medida.
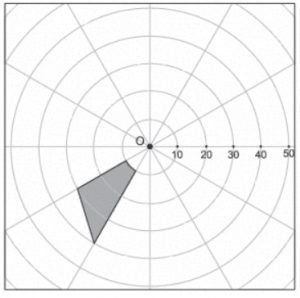
Calcule a área da floresta em chamas indicada pelo radar.
Extraído de UFJF-Modificado.

Lembrete
✐ Conhecidas as medidas [tex]a[/tex] e [tex]b[/tex] de dois lados de um triângulo [tex]ABC[/tex] qualquer e a medida [tex]\alpha[/tex] do ângulo compreendido entre estes lados, a área de [tex]ABC[/tex] é dada por
[tex]\qquad \qquad \boxed{S = \dfrac{1}{2}\cdot a\cdot b\cdot sen \; \alpha}.[/tex]
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus:
[tex]\qquad \qquad \boxed{S_{setor}=\dfrac{\pi\cdot R^{\,2} \cdot \alpha}{360}}.[/tex]
Solução
A área desejada pode ser calculada pela diferença entre as áreas do triângulo [tex]OBA[/tex] (em vermelho) e do setor circular de raio [tex]10[/tex] e centro em [tex]O[/tex] (amarelo).
Observando as marcações das medidas no radar, podemos concluir que [tex]OA=40[/tex] e [tex]OB=30[/tex].
Além disso, como as retas dividem as circunferências em [tex]12[/tex] arcos de mesma medida, temos que [tex]A\hat{O}B=\dfrac{360^\circ}{12}=30^\circ[/tex].
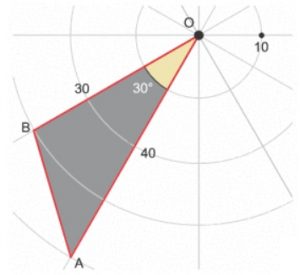
Assim, pelo Lembrete, a área do triângulo é:
[tex]\qquad S_{OBA} =\dfrac{40\cdot30\cdot sen\;30^\circ}{2}=\boxed{300}[/tex]
e a área do setor circular é:
[tex]\qquad S_{setor}=\dfrac{1}{12}\cdot \pi \cdot10^{2}=\boxed{\dfrac{25\pi}{3}}.[/tex]
Portanto, a área [tex]S[/tex] da floresta em chamas é dada por
[tex]\qquad S=300-\dfrac{25\pi}{3}=\dfrac{25}{3}\cdot(36-\pi)\;u.a.[/tex]
Solução elaborada pelos Moderadores do Blog.
