✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir da 1ª série do E. M.)
No plano cartesiano da figura abaixo, no qual os eixos estão graduados em quilômetros, estão representados os gráficos da função
[tex]\qquad f: \left[ 0,\dfrac{5}{2} \right] \rightarrow \mathbb{R}[/tex], definida por [tex]f(x)=\dfrac{-1}{2}x^{2}+\dfrac{5}{2}x[/tex],
e da função afim
[tex]\qquad g: \left[ \dfrac{5}{2}, 5 \right] \rightarrow \mathbb{R}[/tex], cujo coeficiente angular é [tex]- \dfrac{5}{4}[/tex].
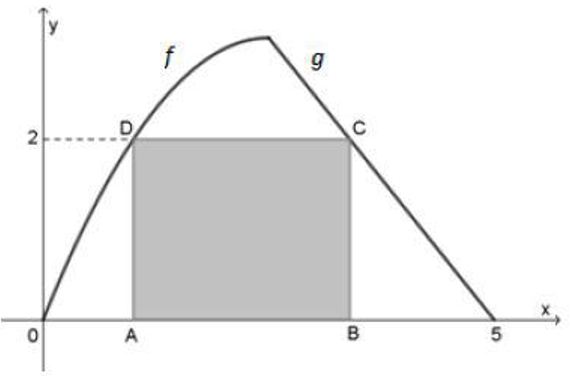
O retângulo [tex]ABCD[/tex] tem os vértices [tex]A[/tex] e [tex]B[/tex] sobre o eixo das abscissas e os vértices [tex]C[/tex] e [tex]D[/tex] sobre os gráficos das funções [tex]g[/tex] e [tex]f[/tex] respectivamente, e ambos possuem ordenadas iguais a [tex]2[/tex].
Qual é a medida da área desse retângulo, em quilômetros quadrados?
Extraído de PISM I.
Solução
A área de um retângulo é calculada pela multiplicação da medida da base pela medida da altura. Pelo enunciado, concluímos que a altura possui medida [tex]2[/tex] km.
Ao fazermos [tex]f(x)=2[/tex], encontramos:
[tex]\quad f(x)=2\\
\quad \dfrac{-1}{2} x^{2}+ \dfrac{5}{2} x=2\\
\quad -x^2+5x=4\\
\quad x^2-5x+4=0.\\
~~[/tex]
Podemos resolver essa última equação do 2º grau utilizando a sua fórmula resolutiva:
[tex]\quad x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\
\quad x=\dfrac{5 \pm \sqrt{25-16}}{2}\\
\quad x=\dfrac{5 \pm 3}{2}\\
\quad x=\dfrac{8}{2}=4 \quad \text{ ou }\quad x=\dfrac{2}{2}=1.[/tex]
Como o domínio da [tex]f[/tex] é o intervalo [tex]\left[ 0, \dfrac{5}{2} \right][/tex], temos como única opção [tex]x=1[/tex].
Portanto, o ponto [tex]A[/tex] tem coordenadas [tex]A=(1,0).[/tex]
Como o gráfico da função [tex]g[/tex] é um segmento de reta que possui coeficiente angular igual a [tex]~-\dfrac{5}{4}[/tex], podemos escrever a lei de formação de [tex]g[/tex] da seguinte maneira:
[tex]\quad g(x)=-\dfrac{5}{4} x+b.[/tex]
Observando o gráfico, vemos que [tex]g(5)=0[/tex]; assim, segue que:
[tex]\quad -\dfrac{5}{4}\cdot 5+b=0\\
\quad b=\dfrac{25}{4}[/tex]
e, portanto, a função [tex]g[/tex] possui a seguinte lei de formação: [tex]\boxed{g(x)=-\dfrac{5}{4}x+\dfrac{25}{4}}.[/tex]
Agora, para descobrirmos o valor da abcissa do ponto [tex]B[/tex], basta fazermos [tex]g(x)=2[/tex]. Observe:
[tex]\quad g(x)=2\\
\quad -\dfrac{5}{4} x+\dfrac{25}{4}=2\\
\quad -5x+25=8\\
\quad x=\dfrac{17}{5}.[/tex]
Com isso, [tex]B= \left( \dfrac{17}{5},0 \right).[/tex]
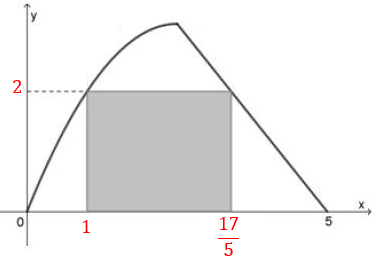
Dessa forma, temos que a medida da base do retângulo [tex]ABCD[/tex] é dada por:
[tex]\quad \dfrac{17}{5}-1= \dfrac{12}{5}=2,4 \text{ km.}[/tex]
Logo, a área desse retângulo mede [tex]2,4 \times 2= \fcolorbox{black}{#eee0e5}{$4,8 \text{ km}^2$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
