Problema
(Indicado a partir do 1º ano do E. M.)
Sabendo-se que a área do triângulo [tex]\triangle{ABC}[/tex] da figura é [tex]\dfrac{24}{25}[/tex] [tex]cm^2[/tex] e que os arcos externos [tex]\stackrel{\textstyle\frown}{\mathrm{AB}}[/tex], [tex]\stackrel{\textstyle\frown}{\mathrm{BC}}[/tex] e o arco [tex]\stackrel{\textstyle\frown}{\mathrm{AC}}[/tex] são semicírculos, calcule a área da região destacada.
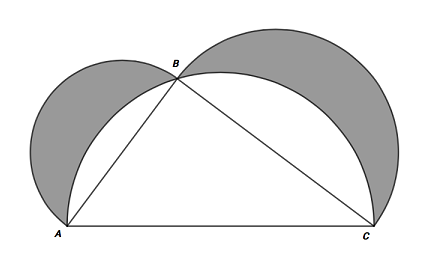
Notação: Na solução deste problema, denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Pelo Teorema do Ângulo Central a medida do ângulo [tex]A\hat{B}C[/tex] é [tex]90^\circ[/tex], já que o segmento [tex]\overline{AC}[/tex] é o diâmetro da circunferência na qual esse ângulo está inscrito. Com isso, o triângulo [tex]\triangle{ABC}[/tex] é retângulo e, como triângulo retângulo chama o Teorema de Pitágoras, temos que [tex] \left(AC\right)^2= \left(AB\right)^2 + \left(BC\right)^2.[/tex]
Dessa forma, se [tex]S_1[/tex] e [tex]S_2[/tex] são as áreas dos dois semicírculos menores e [tex]S_3[/tex] é a área do semicírculo maior, segue que:
[tex] S_1+S_2=\dfrac{\pi}{2}\left(\dfrac{AB}{2}\right)^2+\dfrac{\pi}{2}\left(\dfrac{BC}{2}\right)^2=\dfrac{\pi}{8}\left(AB^2+BC^2\right)=\dfrac{\pi}{8}AC^2=\dfrac{\pi}{2}\left(\dfrac{AC}{2}\right)^2=S_3.[/tex]
(Veja que os raios dos dois semicírculos menores são [tex]\dfrac{AB}{2}[/tex] e [tex]\dfrac{BC}{2}[/tex].)
Daí, sendo [tex]S_4[/tex] a área do triângulo [tex]ABC[/tex], a área [tex]S[/tex] da região destacada é dada por
[tex]S=S_1+S_2+S_4-S_3=(\cancel{S_1+S_2})+S_4-\cancel{S_3}=\boxed{S_4}.[/tex]
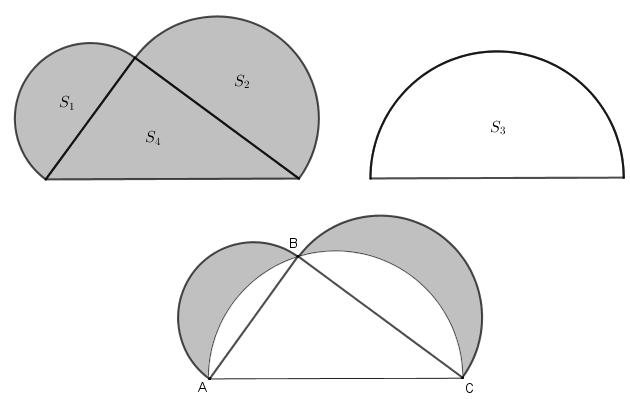
Isto mostra que a área da região destacada é exatamente a área do triângulo [tex]\triangle{ABC}[/tex] e vale, portanto, [tex]\fcolorbox{black}{#eee0e5}{$S=\dfrac{24}{25} \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
