Problema
(Indicado a partir do 1º ano do E. M.)
O triângulo [tex]ABC[/tex], inscrito em uma circunferência [tex]\lambda[/tex], tem o lado [tex]\overline{BC}[/tex] medindo [tex]5[/tex] cm.
Em cada item, determine a área do círculo definido por [tex]\lambda[/tex], sabendo que:
(a) o ângulo oposto ao lado [tex]\overline{BC}[/tex] mede [tex]45^\circ.[/tex]
(b) o ângulo oposto ao lado [tex]\overline{BC}[/tex] mede [tex]22,5^\circ.[/tex]

Lembrete
O Teorema de Pitágoras é um importantíssimo resultado que relaciona as medidas dos lados de um triângulo, mas tem a restrição de poder ser aplicado apenas em triângulos retângulos.
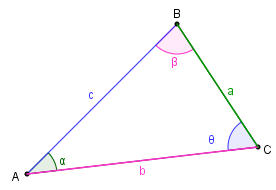
Para triângulos genéricos, as medidas dos lados também podem ser relacionadas por igualdades conhecidas como “Lei dos cossenos”.
Para o triângulo [tex]ABC[/tex] da figura ao lado, a lei dos cossenos garante as seguintes relações entre seus lados e seus ângulos:
[tex]\qquad a^2 = b^2 + c^2 – 2\cdot b\cdot c\cdot cos \, \alpha[/tex];
[tex]\qquad b^2 = a^2 + c^2 – 2\cdot a\cdot c\cdot cos \, β[/tex];
[tex]\qquad c^2 = a^2 + b^2 – 2\cdot a\cdot b\cdot cos \, \theta [/tex].
Solução
Sejam [tex]\lambda[/tex] a circunferência na qual o triângulo [tex]ABC[/tex] está inscrito e [tex]O[/tex] o centro de [tex]\lambda[/tex].
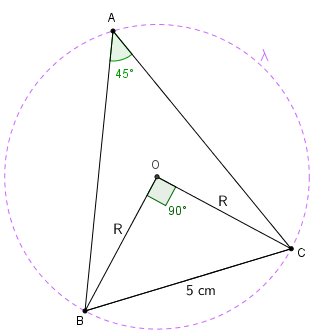
(a) Primeiramente observamos que a medida do ângulo interno [tex]\hat{A}[/tex] é [tex]45 ^\circ[/tex], por hipótese. Observamos também que, como [tex]\hat{A}[/tex] é um ângulo inscrito na circunferência [tex]\lambda[/tex], a medida do ângulo central [tex]B\hat{O}C[/tex] é [tex]90^\circ[/tex], já que esta medida é o dobro da medida do ângulo inscrito [tex]B\hat{A}C[/tex]. (Se você não se lembra desses resultados, visite mais tarde a Sala de Estudos Ângulo Central e Ângulo Inscrito.)
Construindo o triângulo de vértices [tex]B[/tex], [tex]O[/tex] e [tex]C[/tex] obtemos, então, um triângulo retângulo cujas medidas dos lados [tex]\overline{OB}[/tex] e [tex]\overline{OC}[/tex] valem a medida do raio da circunferência; suponha que essa medida seja [tex]R \, cm[/tex] .
Como o triângulo é retângulo, podemos aplicar o Teorema de Pitágoras e obter:
[tex]\qquad 5^2=R^2+R^2[/tex]
[tex]\qquad 25=2R^2[/tex]
[tex]\qquad R^2=\dfrac{25}{2}[/tex],
para em seguida, obtermos a área do círculo definido por [tex]\lambda[/tex]: [tex]\fcolorbox{black}{#eee0e5}{$A=\dfrac{25 \pi}{2} cm^2$} \, [/tex].
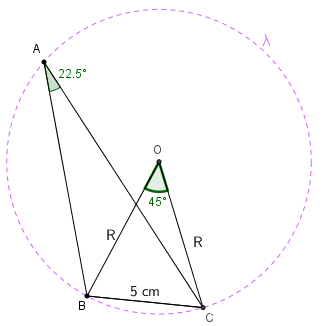
(b) Aqui, o raciocínio inicial é o mesmo do item (a): assim, construímos o triângulo de vértices [tex]B[/tex], [tex]O[/tex] e [tex]C[/tex] e observamos agora que, como a medida do ângulo interno [tex]\hat{A}[/tex] do triângulo [tex]ABC[/tex] é [tex]22,5 ^\circ[/tex], por hipótese, a medida do ângulo oposto ao lado [tex]\overline{BC}[/tex] no triângulo [tex]BOC[/tex] é [tex]45 ^\circ[/tex], já que, mais uma vez, o ângulo [tex]B\hat{O}C[/tex] é o ângulo central relativo a [tex]\lambda[/tex] correspondente ao ângulo inscrito [tex]B\hat{A}C[/tex]. (Se você não se lembra desses resultados, não se esqueça de visitar a Sala de Estudos Ângulo Central e Ângulo Inscrito, mais tarde.)
Agora o triângulo [tex]BOC[/tex] não é retângulo, portanto NÃO podemos aplicar o Teorema de Pitágoras. A finalização deste item será possível com a utilização de uma das igualdades da Lei dos Cossenos; vejamos:
[tex]\qquad 5^2=R^2+R^2-2\times R \times R \times cos(45^\circ )[/tex]
[tex]\qquad 25=2R^2-2R^2\times\dfrac{\sqrt{2}}{2}[/tex]
[tex]\qquad 25=R^2(2-\sqrt2)[/tex]
[tex]\qquad R^2=\dfrac{25}{2-\sqrt{2}}[/tex]
[tex]\qquad R^2=\dfrac{25}{2-\sqrt2}\times\dfrac{2+\sqrt2}{2+\sqrt2}[/tex]
[tex]\qquad R^2=\dfrac{25(2+\sqrt2)}{4-2}[/tex]
[tex]\qquad R^2=\dfrac{25(2+\sqrt2)}{2}[/tex].
Assim, obtemos a área solicitada:[tex] \, \, \fcolorbox{black}{#eee0e5}{$A= \pi\dfrac{25(2+\sqrt{2})}{2} cm^2$}[/tex].
Solução elaborada pelos Moderadores do Blog.
