Problema
(Indicado a partir do 9º ano do E. F.)
Uma neta pergunta à sua avó:
– “Vovó, qual é a sua idade?”
Sendo professora de matemática, a avó responde:
– “Vovô e eu, juntos, temos [tex]140[/tex] anos. E a idade do vovô é o dobro da minha quando ele tinha a idade que eu tenho agora”.
Qual a idade da vovó? Lembre-se de justificar seu resultado.
Solução
Sejam [tex]x[/tex] e [tex]y[/tex] as idades atuais da avó e do avô, respectivamente.
Assim, vamos analisar o problema em dois tempos diferentes:
- no presente, quando as idades da vovó e do vovô são [tex]x[/tex] e [tex]y[/tex];
- no passado, quando o avô tinha a idade que a avó tem agora.
Note que entre esses dois tempos passaram-se [tex](y-x)[/tex] anos.
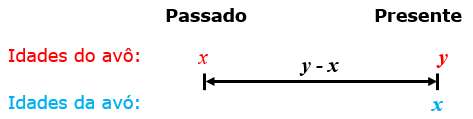
Observe que, [tex](y-x)[/tex] anos atrás, a avó tinha [tex]x-(y-x)[/tex] anos e atualmente o avô tem o dobro dessa idade.
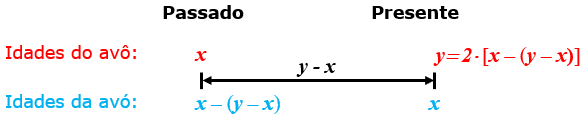
Assim,
[tex]\qquad y = 2\cdot [x-(y-x)]=2\cdot(2x-y)=4x-2y[/tex]
e, portanto, [tex]3y = 4x[/tex].
Sabemos que [tex]x + y = 140[/tex], logo [tex]\boxed{y=140-x}[/tex]. Substituindo esse valor de [tex]y[/tex] em [tex]\boxed{3y=4x}[/tex], temos que:
[tex]\qquad 3\cdot(140-x)=4x \\
\qquad 420-3x=4x \\
\qquad 7x=420 \\
\qquad x=60.[/tex]
Portanto, a vovó tem [tex]60[/tex] anos atualmente.
Solução elaborada pelos Moderadores do Blog .
