Noves fora… Nada?
|
Já ouvi algumas pessoas falando sobre a “prova dos noves”, mas eu não sei o que isso significa! |
 |
 |
Topa uma pequena discussão para tentarmos entender a manha e a arte da tal artimanha? |
|
Vamos lá! |
 |
A artimanha
Papel e caneta, três números escritos e a soma realizada:
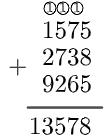
Como se tira a prova dos noves? Basta que você vá somando os algarismos das parcelas, subtraindo [tex]9[/tex] sempre que a soma igualar ou ultrapassar esse valor. A linguagem costuma ser mais ou menos assim:
“Um mais cinco, seis; mais sete, treze. Nove fora, quatro. Quatro mais cinco, nove. Nove fora, nada. (próxima parcela) Dois mais sete, nove. Nove fora, nada. Três mais oito, onze. Nove fora, dois. (próxima parcela) Dois mais nove, onze. Nove fora, dois. Dois mais dois, quatro; mais seis, dez. Nove fora, um. Um mais cinco, seis.”
Agora faça o mesmo com os algarismos do total:
“Um mais três, quatro; mais cinco, nove. Nove fora, nada. Sete mais oito, quinze. Nove fora, seis.”
O resultado foi o mesmo? Isso quer dizer que a soma foi realizada corretamente!
… Será?…
Um Pouco de História
Antigamente, a prova dos noves fez parte dos conteúdos dos livros didáticos e dos livretos de tabuadas. Ela também era conhecida como “noves-fora”, mas deixou de ser usada nas escolas com o passar dos anos, embora ainda seja aplicada, principalmente, por comerciantes.
Alguns indícios apontam que este método é encontrado nas obras de vários escritores e matemáticos árabes, incluindo Al-Khwarizmi (falecido em 825). O filósofo Avicenna (falecido em 1037) trata deste método como um método hindu. Porém, muito antes do que isso, no século III, o teólogo Hipólito de Roma foi mencionado por ter dado os métodos da prova de um cálculo denominado noves e setes-fora.
As figuras a seguir mostram um livro didático brasileiro de 1902, no qual o conteúdo da prova dos noves era ensinado, embora o autor tenha dito, em certo ponto, que os resultados “podiam ser negativos” (no sentido de equivocados):


Uma pesquisa histórica mais completa e com todas as referências pode ser consultada no artigo Lacava, A. G., & da Costa, D. A. (2016) (acesso em 16 jul 24).
Em termos mais formais…
Considere as propriedades [tex]A[/tex] (o resultado dos “noves fora” foi o mesmo nas parcelas e no total) e [tex]B[/tex] (a conta foi feita de forma correta).
A prova dos noves afirma que [tex]A\iff B[/tex] ([tex]A[/tex] equivale a [tex]B[/tex]), ou seja:
- que [tex]A\Longrightarrow B[/tex] ([tex]A[/tex] implica [tex]B[/tex])
- e que [tex]B\Longrightarrow A[/tex] ([tex]B[/tex] implica [tex]A[/tex]), o que poderia também ser simbolizado por [tex]A\Longleftarrow B[/tex].
Em palavras, essas duas implicações querem dizer, respectivamente, que:
- Se o resultado dos “noves fora” foi o mesmo nas parcelas e no total, então a conta foi feita de forma correta.
- Se a conta foi feita de forma correta, então o resultado dos “noves fora” foi o mesmo nas parcelas e no total.
Mas… Você pode testar manualmente (ou “calculadoramente” se estiver com muita pressa) que, no nosso exemplo inicial, a prova dos [tex]9[/tex] validaria as seguintes somas incorretas:
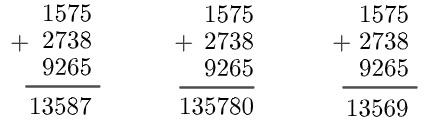
e muitas outras…
O que está acontecendo aqui?!
Inicialmente, observe que
[tex]\qquad 13587=13578+9\cdot1[/tex],
[tex]\qquad 135780=13578+9\cdot13578[/tex],
[tex]\qquad 13569=13578+9\cdot(-1) [/tex].
De fato, se você continuar testando resultados, irá perceber que a prova dos noves funciona sempre que o resultado obtido for diferente do resultado correto por um múltiplo de [tex]9[/tex].
Estes testes descartam “de cara” a primeira implicação: não é verdade que “Se o resultado dos “noves fora” foi o mesmo nas parcelas e no total, então a conta foi feita de forma correta”.
De fato, apenas a segunda implicação é válida. Mas por que a prova dos [tex]9[/tex] foi tão utilizada? Por que o [tex]9[/tex], afinal? E como garantir a segunda implicação?
Vamos tentar entender o que está acontecendo aqui.
Primeiro, vamos relembrar o critério de divisibilidade por [tex]9[/tex] a partir de um exemplo simples:
Considere um número de três algarismos, escrito no sistema decimal como [tex]abc[/tex] (por exemplo, o número [tex]123[/tex] é obtido fazendo [tex]a=1, b=2, c=3[/tex]).
Pelo Algoritmo da Divisão, [tex]abc=9\cdot q+r[/tex], para um único par de números naturais [tex]q[/tex] e [tex]r[/tex], com [tex]0\le r\lt9[/tex]. O número [tex]q[/tex] é o quociente da divisão de [tex]abc[/tex] por [tex]9[/tex] e [tex]r[/tex] é o resto desta divisão.
Então, temos:
[tex]\qquad abc=9\cdot q+r, \\
\qquad 100\cdot a+10\cdot b+c=9\cdot q+r, \\
\qquad 99\cdot a+9 \cdot b+a+b+c=9\cdot q+r, \\
\qquad 9\cdot(11a+b)+a+b+c=9\cdot q+r, \\
\qquad a+b+c=9\cdot(q-11a-b)+r, \\
\qquad a+b+c=9\cdot q_0+r,[/tex]
para determinado número inteiro não negativo [tex]q_0=q-11a-b[/tex].
Mas [tex]a+b+c=9\cdot q_0+r[/tex], com [tex]0\le r\lt9[/tex], indica, pela unicidade do quociente e do resto no Algoritmo da divisão, que [tex]r[/tex] é o resto da divisão de [tex]a+b+c[/tex] por [tex]9[/tex]. Portanto, o resto da divisão de [tex]abc[/tex] por [tex]9[/tex] é o mesmo resto da divisão de [tex]a+b+c[/tex] por [tex]9[/tex]. Algo análogo pode ser feito para números de dois, quatro, cinco, …, qualquer quantidade de algarismos!
Ou seja, o resto de [tex]a_na_{n-1}\cdots a_1a_0[/tex] (onde os [tex]a_i'[/tex]s são os dígitos do número no sistema decimal) e de [tex]a_n+a_{n-1}+\cdots +a_1+a_0[/tex] na divisão por [tex]9[/tex] é o mesmo.
Esta regra, inclusive, pode ser aplicada quantas vezes forem necessárias. Por exemplo, o resto da divisão de [tex]8\,765\, 891[/tex] por [tex]9[/tex], é o mesmo resto da divisão de [tex]8+7+6+5+8+9+1=44[/tex] por [tex]9[/tex], que é o mesmo resto da divisão de [tex]4+4=8[/tex] por [tex]9[/tex], que é… [tex]8[/tex], é claro.
Você sabia?
A raiz digital de um número natural é definida como o resultado do processo de somar recursivamente os dígitos até que só reste um algarismo. Ela também pode ser chamada de soma repetida dos dígitos deste número. Assim, pelo que vimos, a raiz digital de [tex]8\,765\, 891[/tex] é [tex]8[/tex].
Particularmente, para que o resto seja nulo, ou seja, o número seja divisível por [tex]9[/tex], é necessário e suficiente que a soma de seus algarismos seja divisível por [tex]9[/tex]. Utilizando este resultado de forma recursiva, um número inteiro é divisível por [tex]9[/tex] se, e somente se, sua raiz digital é [tex]9[/tex].
Muito bem. Agora, vamos analisar a primeira parte da prova dos noves, ou seja, os “noves fora” com os algarismos das parcelas.
Observe que os algarismos são somados até um primeiro resultado maior que [tex]9[/tex], algo da forma [tex]9+n_1[/tex], sendo [tex]n_1[/tex] um inteiro tal que [tex]0 \le n_1 \lt 9[/tex]. Em seguida, subtrai-se o [tex]9[/tex] e soma-se o [tex]n_1[/tex] com os demais algarismos até obter algo da forma [tex]9+n_2[/tex], com [tex]n_2[/tex] inteiro e [tex]0 \le n_2 \lt 9[/tex].
Se deixássemos para subtrair os “noves” no final de cada parcela, o que não faria a menor diferença, devido à propriedade comutativa da adição, estaria explícito o seguinte processo:
- Soma-se todos os algarismos da parcela em questão.
- Subtrai-se o maior múltiplo de [tex]9[/tex] menor ou igual à soma encontrada.
Foque sua atenção no fato de que o resultado de cada processo equivale ao resto deixado pela parcela na divisão por [tex]9[/tex]. Ao final, somamos todos estes resultados e subtraímos o maior múltiplo de [tex]9[/tex] menor ou igual a este último total.
Considere, por exemplo, três inteiros positivos [tex]x, y[/tex] e [tex]z[/tex]. Pelo Algoritmo da Divisão, temos, para [tex]q_i[/tex] e [tex]r_i[/tex] naturais únicos em cada caso, sendo [tex]0\le r_i\lt9[/tex]:
[tex]\qquad x=9\cdot q_1+r_1[/tex];
[tex]\qquad y=9\cdot q_2+r_2[/tex] e
[tex]\qquad z=9\cdot q_3+r_3[/tex].
Na primeira parte da prova dos [tex]9[/tex] para a soma desses números, obtemos [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex], sendo o resultado final determinado e único [tex]r_4[/tex], tal que [tex]r_1+ r_2+ r_3=9\cdot q_4+ r_4[/tex]. Note que [tex]x+y+z=9\cdot (q_1+q_2+q_3+q_4)+r_4[/tex] e que [tex]r_4[/tex] é o resto da divisão de [tex]x+y+z[/tex] por [tex]9[/tex].
A segunda parte da prova dos noves consiste em realizar este mesmo processo no total obtido com a soma. Sendo [tex]S[/tex] esse total, o resultado será [tex]r_5[/tex], tal que [tex]S=9\cdot q_5 + r_5[/tex]. A prova dos noves consiste, resumidamente, em verificar se [tex]r_4=r_5[/tex].
Ora, como devemos ter [tex]x+y+z=S[/tex], está claro que, SE a soma estiver correta, ENTÃO [tex]r_4= r_5[/tex]. De fato, se [tex]9\cdot(q_1+q_2+q_3+q_4)+r_4=9\cdot q_5+r_5[/tex] com [tex]q_i,r_i\in\mathbb{Z}, 0\le r_i\lt9[/tex], a unicidade do quociente e do resto no Algoritmo da Divisão garante que [tex]r_4=r_5[/tex]. Porém, essa igualdade também pode ocorrer em infinitos casos nos quais [tex]r_4=r_5[/tex], mas [tex]q_1+q_2+q_3+q_4\not= q_5[/tex], a saber, nos casos em que [tex]q_1+q_2+q_3+q_4+k = q_5[/tex], com [tex]k[/tex] inteiro não nulo. Observe que, nestes casos,
[tex] \qquad S=9\cdot q_5+r_5=9\cdot(q_1+q_2+q_3+q_4+k)+r_5\\
\qquad S=9\cdot(q_1+q_2+q_3+q_4+k)+r_4\\
\qquad S=9\cdot(q_1+q_2+q_3+q_4)+r_4\textcolor{red}{+9k}\not=9\cdot(q_1+q_2+q_3+q_4)+r_4 \text{(resultado correto)}[/tex]
E o que acontece? Em casos assim a soma não está correta e a prova dos [tex]9[/tex] nos remete um falso positivo, como vimos nos nossos exemplos!
Voltando às propriedades [tex]A[/tex] e [tex]B[/tex], provamos que [tex]B\Longrightarrow A[/tex], pois, se a soma estiver correta, os restos da soma das parcelas e do total na divisão por [tex]9[/tex] será o mesmo. Assim, um resultado invalidado pela prova dos noves nunca pode estar correto, isto é, não existem “falsos negativos”.
Mas, [tex]A\Longrightarrow B[/tex] é uma implicação falsa para qualquer resultado errado cuja distância ao resultado correto seja um múltiplo de [tex]9[/tex].
|
Humm, entendi! Mas por que a prova ficou tão famosa? E por que o [tex]9[/tex] e não o [tex]3[/tex]? Afinal, o critério de divisibilidade por [tex]3[/tex] também envolve a soma dos algarismos do número, não é? |
 |
Sim, poderíamos criar, em termos muito semelhantes, a “prova dos três”. Entretanto, nesse caso, a prova remeteria um falso positivo em todas as ocorrências nas quais o resultado encontrado distasse do correto um múltiplo de [tex]3[/tex] não nulo. Assim, [tex]13\,575[/tex] e [tex]13\,581[/tex], por exemplo, seriam resultados aceitos na soma tomada como modelo. Contudo, esses resultados seriam eliminados pela “prova dos noves”. Mais especificamente, a cada três falsos positivos remetidos pela “prova dos três”, a “prova dos nove” localizaria dois erros, o que a torna melhor, ou menos pior.
É possível, ainda, supor que a escolha do [tex]9[/tex] teve um caráter mais estético e simplificador pelo seguinte motivo: A soma de dois algarismos, sendo o primeiro diferente de [tex]9[/tex] (do contrário bastaria fazer o “nove fora” e passar para o próximo algarismo), é menor que [tex]18=9 \times 2[/tex]. Dessa forma, no processo utilizado, cada “nove fora” deixa, com certeza, um número menor que [tex]9[/tex], ou seja, nunca precisamos subtrair o [tex]9[/tex] mais de uma vez a cada etapa. Isso não ocorre com o [tex]3[/tex] e basta tentar utilizar a “prova dos três” na soma do exemplo para encontrar, de início, “um mais cinco, seis”, para o qual precisaríamos fazer o “três fora” duas vezes.
Sobre uma possível explicação para a popularidade da prova dos noves, observe que, a cada nove possíveis resultados errados, ela detecta oito deles. Isso equivale a aproximadamente 89% – não é tão ruim, certo? Particularmente, ela detecta qualquer erro pequeno (menor que 9 unidades).
Isso também significa que, se [tex]A[/tex] não acontecer, então [tex]B[/tex] também não acontece. De fato, utilizando os termos da lógica matemática, a fórmula proposicional [tex]p\to q[/tex] (se [tex]p[/tex], então [tex]q[/tex]) é equivalente à sua contrapositiva [tex]~q\to ~p[/tex] (se não [tex]q[/tex], então não [tex]p[/tex]).
Por isso muitos comerciantes ainda usam essa técnica do “noves fora”: se a prova dos noves der errado, a conta também está errada. E, a cada nove possíveis resultados errados, esta prova detecta oito deles.
Como já indicado, para entender um pouco mais sobre a linguagem da lógica matemática, você pode dar uma passadinha pela Sala de Estudo: Um pouco sobre a linguagem matemática.
|
Aprendi bastante com essa discussão novítica. |
 |
 |
Aliás, percebeu que trocas de posições dos algarismos de um número não alteram o resto de sua divisão por [tex]9[/tex]? |
|
Será?! |
 |
 |
Sim, em decorrência da propriedade comutativa da adição. |
|
Que bacana! |
 |
Alguns exercícios para assimilar melhor nossa discussão
1) A professora Raiane pediu que seus alunos somassem os números [tex]12345,67890,45678[/tex]. Rhana entregou [tex]125823[/tex] como resposta. Raquel encontrou [tex]125958[/tex]. Raimundo, por sua vez, respondeu [tex]125928[/tex].
(a) Todos os resultados estão incorretos. Utilize a prova dos noves para eliminar uma destas respostas. Conclua que esta prova não foi suficiente para invalidar duas das três respostas incorretas.
(b) O resultado correto da soma que Raiane propôs é [tex]125913[/tex]. Escreva este número na forma [tex]9\cdot q+r[/tex], com [tex]q,r\in\mathbb{N}[/tex], [tex]0\le r\lt9[/tex]. Verifique que os dois resultados incorretos que não foram invalidados pela prova dos noves são da forma [tex]9\cdot q’+r[/tex], com o mesmo [tex]r[/tex].
2) Encontre os restos das seguintes divisões:
(a) [tex]2346128823479[/tex] por [tex]9[/tex]
(b) [tex]4236128823479[/tex] por [tex]9[/tex]
(c) [tex]2346128823479[/tex] por [tex]3[/tex]
(d) [tex]4236128823479[/tex] por [tex]3[/tex]
3) Você sabia que a prova dos noves para outras operações também era ensinada nas escolas? Veja um exemplo quanto à multiplicação, extraído do já citado livro “Arithmetica Primaria” de Cezar Pinheiro (1902):

O número [tex]2[/tex] representa o noves-fora do multiplicando, o número [tex]4[/tex] equivale ao noves-fora do multiplicador, o número [tex]8[/tex] ao lado do quatro representa o noves-fora do produto ([tex]2 \times 4[/tex]), o número [tex]8[/tex] ao lado do número dois representa o noves-fora do resultado. Como ambos coincidem, de acordo com a prova dos noves, a operação está correta. Discuta esta prova!
|
Gostei! |
 |
 |
Quem disse que a sala acabou? Chegou a hora da matemágica! |
Truques matemágicos
Este vídeo apresenta um truque de adivinhação, utilizando a raiz digital de um número.
Para assistir, é só clicar na setinha.

Matemática Rio, de Rafael Procópio.
|
Uau! Vou pensar em alguns outros truques com os critérios de divisibilidade por [tex]3[/tex] e por [tex]9[/tex]. |
 |
 |
Não são apenas esses critérios que geram boas matemágicas! Divirta-se com o seguinte exemplo: |
- Ele pede para uma pessoa na plateia pensar em um número de sete algarismos. Esse número não deve ser revelado.
- Então pede para ela inverter o número (primeiro algarismo vira o último, o segundo vira o penúltimo e assim por diante) e subtrair o maior do menor (pode usar lápis e papel, pois a conta é grande). Nada é revelado ainda.
- Finalmente pede para a pessoa convidada ir falando na ordem os sete algarismos obtidos (mesmo os possíveis zeros à esquerda devem ser falados), sendo que um dos algarismos ela não deve dizer, desafiando Mister R. com “Descubra!”.
- Após o convidado concluir a sua participação, para espanto de todos, Mister R. imediatamente diz o algarismo que ele não falou.
Por exemplo:
- A pessoa escolhe o número [tex]2485772[/tex].
- O número invertido é [tex]2775842[/tex]. Subtraindo: [tex]2775842 – 2485772 = 0290070[/tex].
- O convidado, então, diz Zero, Dois, Nove, Zero, Zero, Descubra!, Zero.
- E o triunfante Mister R., diz de imediato “Sete!”, recebendo as suas merecidas palmas.
O segredo de Mister R. é que ele sabe que o número obtido após a subtração deve ser múltiplo de onze. E sabe também o critério de divisibilidade por onze: Seja [tex]a_k a_{k-1}\cdots a_2a_1a_0[/tex] a representação decimal de um número inteiro [tex]n[/tex]. O número [tex]n[/tex] é múltiplo de [tex]11[/tex] se, e somente se, [tex] (a_0+a_2+a_4+\cdots)-(a_1+a_3+a_5+\cdots)[/tex] é múltiplo de [tex]11[/tex].
Por exemplo: [tex]4\,770\,216[/tex] é múltiplo de [tex]11[/tex], pois [tex](6+2+7+4) -(1+0+7) = 11[/tex] é um múltiplo de [tex]11[/tex]; já [tex]5\,672\,109[/tex] não é múltiplo de [tex]11[/tex], pois [tex](9 + 1 + 7 + 5) – (0 + 2 + 6) = 14[/tex] não é múltiplo de [tex]11[/tex].
Explicando o truque: [tex]0290070[/tex] é múltiplo de [tex]11[/tex], pois [tex](0 + 0 + 9 + 0) – (7 + 0 + 2) = 0[/tex] que é múltiplo de [tex]11[/tex].
a) Por que o resultado deve ser divisível por [tex]11[/tex]?
b) Um membro da plateia disse: Quatro, Três, Dois, Zero, Descubra!, Cinco, Cinco.
Faça como o grande Mister R. e determine o algarismo que falta.
c) Outro membro da plateia disse: Seis, Zero, Oito, Descubra!, Zero, Oito, Quatro. Mister R., para surpresa de todos, afirmou que não diria o algarismo porque o resultado da conta estava errado! Baseado no critério de divisibilidade por onze, explique mais esse mistério envolvendo o maior dos matemágicos.

Equipe COM – OBMEP
