M_Sala de ajuda: Funções – Esboçando a definição

Funções
Esboçando a definição

Os primeiros contatos que temos com as funções ocorrem nos últimos anos do Ensino Fundamental. Lá somos informados de que o conceito de função é um dos mais importantes não só em matemática como também em outras áreas, já que as funções permitem relacionar grandezas segundo uma relação de dependência e com isso é possível, de certa forma, visualizar mudanças sofridas por uma grandeza a partir da “variação” de outra grandeza da qual a primeira é dependente. Fenômenos físicos, químicos, biológicos, econômicos ou sociais, entre outros, necessitam desse objeto matemático.

Mas, matematicamente, que objeto é esse que vamos estudar?

Bom, se neste momento a cada um de vocês fosse perguntado

• “O que é uma função?”

a grande maioria responderia algo do tipo

• “Uma função é uma regra que a cada elemento de um conjunto relaciona, de modo único, um elemento de um segundo conjunto. Por exemplo [tex]f(x)=x^2[/tex].”

Como essa seria a resposta de muitos de vocês, vamos iniciar a nossa discussão sobre o objeto matemático função dizendo que esta não é uma definição formal de função. Vamos justificar por quê.

✐ Se função fosse meramente uma regra, as funções [tex]f, \, g, \, h, \, l \, [/tex] abaixo definidas, obtidas pela aplicação da regra [tex]\boxed{ x \mapsto x^2}[/tex] a conjuntos específicos, seriam iguais; e elas não são iguais.

[tex]\begin{array}{c|c|c|c}
f:\{-2,0,2\}\rightarrow\{0,4\}&g:\{0,2\}\rightarrow\{0,2,4\}&h:\{-2,0,2\}\rightarrow\{0,2,4\}&l:\{0,2\}\rightarrow\{0,4\}\\
\boxed{f(x)=x^2}&\boxed{g(x)=x^2}&\boxed{h(x)=x^2}&\boxed{l(x)=x^2}
\end{array}[/tex]

Vamos explorar [tex]f, \, g, \, h, \, l \, [/tex] utilizando diagramas de Venn.

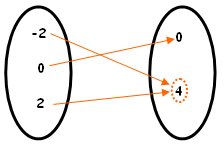
(1) [tex]f:\{-2,0,2\}\rightarrow\{0,4\}\\f(x)=x^2[/tex] Observem que a regra [tex]\boxed{ x \mapsto x^2}[/tex] está associando a dois elementos distintos, [tex]-2[/tex] e [tex]2[/tex], um único elemento, [tex]4[/tex]. Uma função que tenha essa característica não tem uma propriedade que vamos definir como injetividade (Um objeto do segundo conjunto não pode estar associado a dois objetos distintos do primeiro conjunto).

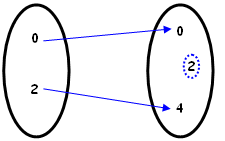
(2) [tex]g:\{0,2\}\rightarrow\{0,2,4\}\\g(x)=x^2[/tex] Observem que a regra [tex]\boxed{ x \mapsto x^2}[/tex] não está associando elementos ao número [tex]2[/tex]. Uma função que tenha essa característica não tem uma propriedade que vamos definir como sobrejetividade (Todo objeto do segundo conjunto deve estar associado a um objeto do primeiro conjunto).

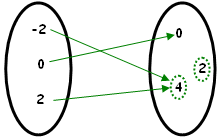
(3) [tex]h:\{-2,0,2\}\rightarrow\{0,2,4\}\\h(x)=x^2[/tex] Aqui, a regra [tex]\quad x \mapsto x^2[/tex] está apresentando simultaneamente as situações listadas em (1) e (2).

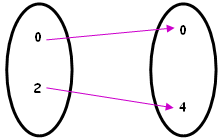
(4) [tex]l:\{0,2\}\rightarrow\{0,4\}\\l(x)=x^2[/tex] Aqui, a regra [tex]\quad x \mapsto x^2[/tex] está apresentando simultaneamente as propriedades que vamos definir como injetividade e sobrejetividade.

Percebam que a regra [tex]x \mapsto x^2[/tex] provocou estruturalmente quatro situações distintas, pois com a mesma regra obtivemos funções com propriedades distintas:

• [tex]f[/tex] é o que definiremos como uma função que não é injetora, mas é sobrejetora;
• [tex]g[/tex] é o que definiremos como uma função que não é sobrejetora, mas é injetora;
• [tex]h[/tex] é o que definiremos como uma função que não é injetora e nem sobrejetora;
• [tex]l[/tex] é o que definiremos como uma função simultaneamente injetora e sobrejetora.

Pelos exemplos fica claro que função não é uma regra, pois um objeto matemático não pode ter uma propriedade hoje e amanhã não tê-la, não é mesmo? Então, como temos interesse matemático ao estudar funções, não podemos adotar como definição que função é apenas uma regra.
Podemos observar que foram os conjuntos nos quais a regra [tex]x \mapsto x^2[/tex] foi aplicada que provocaram comportamentos estruturais diferentes; dessa forma, na definição formal de função temos que levar em conta três componentes: dois conjuntos não vazios e uma regra que permita associar a cada elemento do primeiro conjunto um e somente um elemento do segundo conjunto.
Para efeito do que será discutido daqui em diante, podemos entender que:

Uma função consiste de dois conjuntos não vazios [tex]A[/tex] e [tex]B[/tex] e uma lei, ou regra, que permite associar a cada elemento [tex]x \in A[/tex] um único elemento [tex]y \in B[/tex]. Neste caso, o conjunto [tex]A[/tex] é dito o domínio da função e, o conjunto [tex]B[/tex], o contradomínio da função.

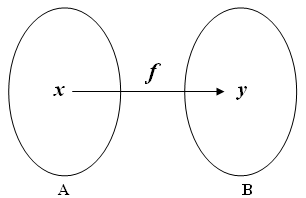
Usaremos a notação
[tex]\qquad f:A \rightarrow B\\
\qquad \quad \, \, x \mapsto y [/tex]
para indicar que [tex]f[/tex] é a função de [tex]A[/tex] em [tex]B[/tex] que faz corresponder a [tex]x[/tex] o valor [tex]y[/tex]. É usual representar o único elemento [tex]y[/tex] associado a [tex]x[/tex] por [tex]f(x)[/tex].

Vocês podem perceber que a notação sugerida coincide com a notação que vocês utilizaram quando aprenderam funções lá no Ensino Fundamental (inclusive utilizamos essas notações nos quatro exemplos apresentados); o único cuidado é assimilar que função não é uma regra e sim uma terna [tex]\left(A, \, B, \, \mapsto\right) [/tex], na qual [tex]A[/tex] e [tex]B[/tex] são conjuntos não vazios e [tex] \, \mapsto[/tex] é a regra que, até então, alguns de vocês chamavam de função. Assim, digam uma função [tex]f[/tex] e não uma função [tex]f(x)[/tex], pois [tex]f(x)[/tex] é a regra que define a função [tex]f[/tex] e, portanto, o valor que a função [tex]f[/tex] assume em um ponto genérico [tex]x[/tex] do seu domínio.
Uma situação especial, e que encontramos com bastante frequência em livros de matemática, ocorre quando dois conjuntos não vazios [tex]X[/tex] e [tex]Y[/tex] estão fixados e vamos definir uma função de um dos conjuntos no outro. Como para se definir uma função precisamos de dois conjuntos e uma regra, se os conjuntos estão fixados, então podemos dizer que uma função [tex]f[/tex] de [tex]X[/tex] em [tex]Y[/tex] é uma regra que a cada elemento [tex]x \in X[/tex] associa um único elemento [tex]y \in Y[/tex].

Perceberam a diferença?

Trata-se, simplesmente, de dois objetos matemáticos distintos:

"função" e "função do conjunto [tex]X[/tex] no conjunto [tex]Y[/tex]".

Com a cabeça preparada, acessem o material sobre funções que disponibilizaremos na plataforma MENTORES.

Bons estudos!!!

Equipe COM – OBMEP