Problema
(Indicado a partir do 8º ano do E. F.)
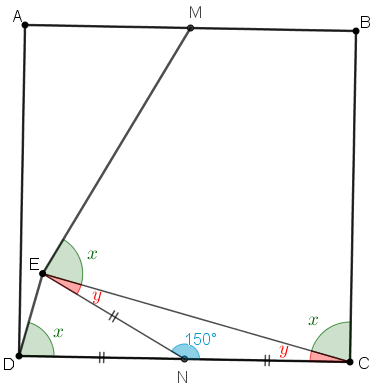
Na figura, [tex]ABCD[/tex] é um quadrado e [tex]M[/tex] é o ponto médio do lado [tex]\overline{AB}[/tex].
Determine o valor de [tex]x[/tex] em graus.
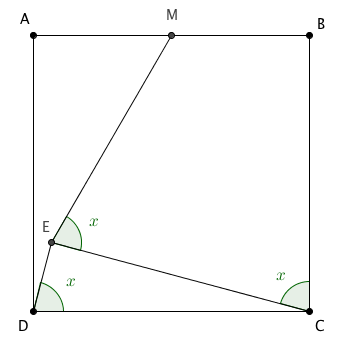
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].

Lembretes
(1) A mediana relativa à hipotenusa de um triângulo retângulo mede a metade do comprimento da hipotenusa.
(2) Se um triângulo retângulo possui um cateto que é metade da hipotenusa, então o ângulo adjacente a esse cateto mede [tex]60^{\circ}.[/tex]
(3) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
Solução
Considere [tex]2a[/tex] como a medida do lado do quadrado [tex]ABCD[/tex].
- Como [tex]B\hat{C}D[/tex] é um ângulo reto, se [tex]y[/tex] for a medida do ângulo [tex]E\hat{C}D[/tex], temos [tex]\boxed{x + y = 90^{\circ}}[/tex] e, com isso, [tex]C\hat{E}D[/tex] é um ângulo reto.
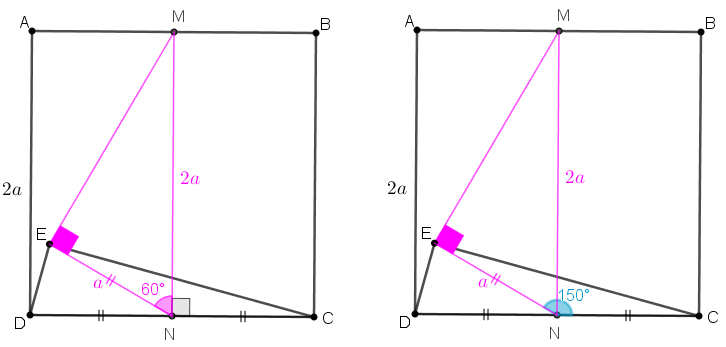
- Ao traçarmos a mediana [tex]\overline{EN}[/tex] do triângulo retângulo [tex]CED[/tex] relativa à hipotenusa, pelo Lembrete (1), temos [tex]EN = DN = CN = \dfrac{2a}{2}=a[/tex].
- Agora, vamos traçar o segmento [tex]\overline{MN}[/tex]. Como [tex]\overline{MN} // \overline{BC}[/tex], temos [tex]MN= 2a[/tex].
- o ângulo [tex]N\hat{E}M[/tex] é reto,
- [tex]MN = 2a[/tex],
- [tex]EN = a[/tex],
- Veja agora que, como [tex]\overline{MN} // \overline{BC}[/tex], o ângulo [tex]M\hat{N}C[/tex] é reto e, portanto, a medida do ângulo [tex]C\hat{N}E[/tex] é [tex] 90^{\circ}+60^{\circ}=150^{\circ}.[/tex]
- Vamos observar mais uma vez o triângulo isósceles [tex]CNE[/tex]. Utilizando o Lembrete (3), obtemos que [tex]y+150^{\circ}+y= 180^{\circ}[/tex] e, portanto, [tex]\boxed{y = 15^{\circ}}[/tex].
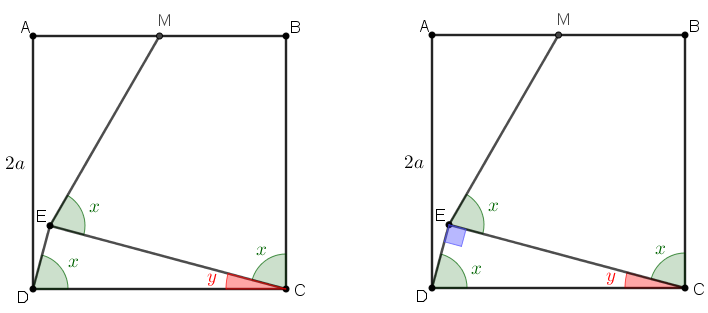
Sendo o triângulo [tex]CNE[/tex] isósceles, temos que a medida do ângulo [tex]C\hat{E}N[/tex] é [tex]y[/tex] e, portanto, a medida do ângulo [tex]N\hat{E}M[/tex] é [tex]x+y= 90^{\circ}.[/tex]
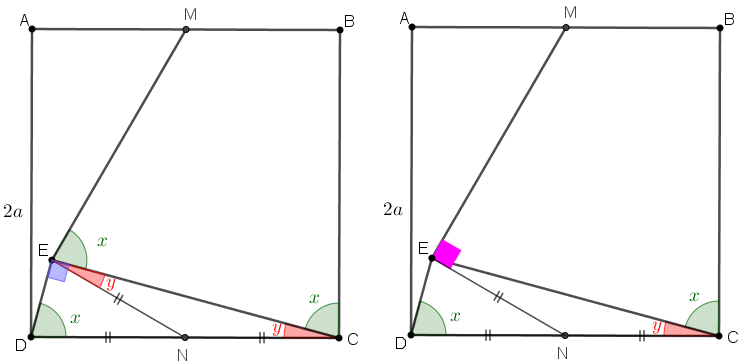
Veja que:
assim, o triângulo [tex]NEM[/tex] é retângulo e possui um cateto que é metade da hipotenusa. Dessa forma, o Lembrete (2) nos permite concluir que a medida do ângulo [tex]M\hat{N}E[/tex] é [tex]60^\circ[/tex].
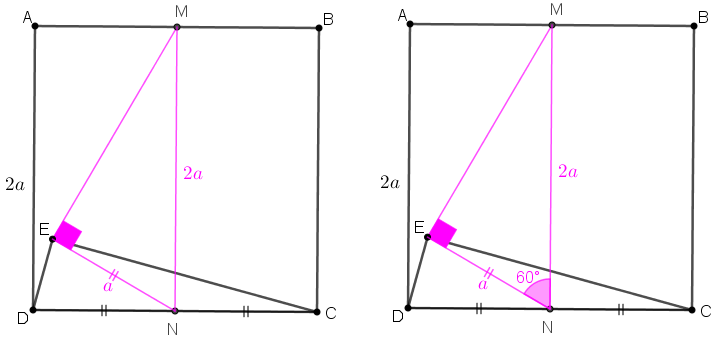
Finalmente, como [tex]\boxed{x+y= 90^{\circ}}[/tex], concluímos que [tex]\fcolorbox{black}{#eee0e5}{$x = 75^{\circ}$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo desta página em PDF. Mas, para abrir esse arquivo, é necessário que você tenha o Adobe Acrobat Reader instalado no dispositivo que você está utilizando. Caso não tenha, é só clicar AQUI para fazer o download. |
