Problema
(Indicado a partir do 9º ano do E. F.)
No quadrilátero [tex]ABCD[/tex] a seguir têm-se [tex]AB=42\;[/tex]cm, [tex]BC=48\;[/tex]cm, [tex]CD=64\;[/tex]cm e [tex]DA=49\;[/tex]cm, sendo [tex]P[/tex] o ponto de interseção das diagonais [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex].
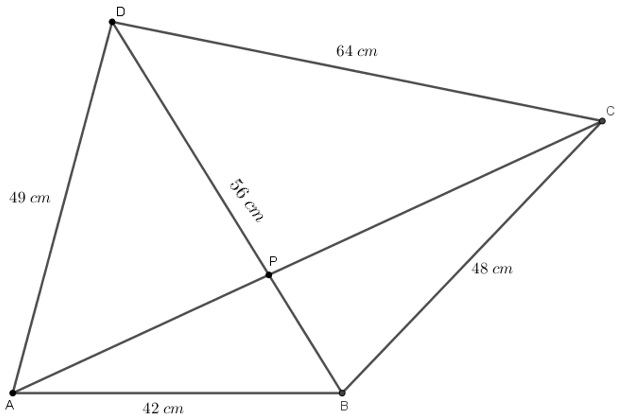
Qual a razão entre os comprimentos dos segmentos [tex]\overline{AP}[/tex] e [tex]\overline{PC}[/tex], sabendo-se que o comprimento da diagonal [tex]\overline{BD}[/tex] é [tex]56\;[/tex]cm?

Lembretes
(1) Caso de semelhança L.L.L. (lado – lado – lado): Se os três lados de um triângulo são proporcionais aos três lados de outro triângulo, então os dois triângulos são semelhantes. (Se você não se lembra dos casos de semelhança de triângulos, clique AQUI.)
(2) Teorema da Bissetriz Interna: A bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes. Na figura abaixo, se [tex]\overline{AD}[/tex] é bissetriz, então [tex]\dfrac{BA}{AC}=\dfrac{BD}{DC}.[/tex]
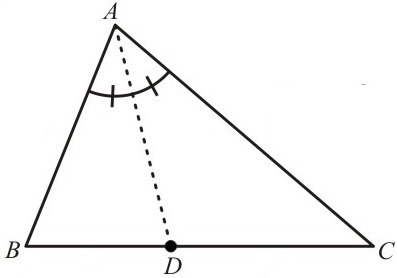
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB[/tex].
Solução
Vamos desenhar e analisar separadamente os triângulos [tex]ADB[/tex] e [tex]BDC[/tex].
Note que podemos reescrever os comprimentos dos lados do triângulo [tex]ADB[/tex] como: [tex]AB=6\cdot7[/tex], [tex]BD=8\cdot7[/tex] e [tex]DA=7\cdot7[/tex].
De modo análogo, no triângulo [tex]BCD[/tex] temos: [tex]BC=6\cdot8[/tex], [tex]CD=8\cdot8[/tex] e [tex]DB=7\cdot8[/tex].
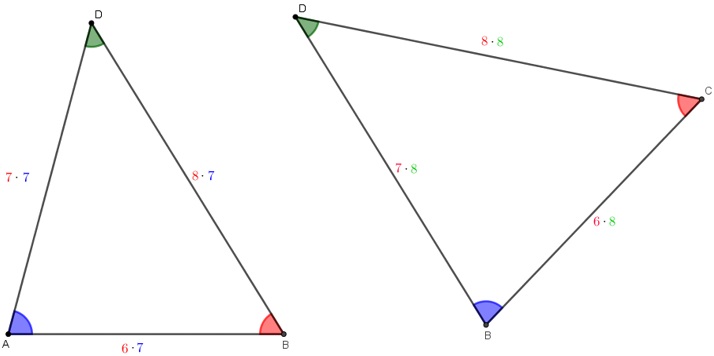
Repare que os dois triângulos possuem os comprimentos de seus lados proporcionais às medidas [tex]6[/tex], [tex]7[/tex] e [tex]8[/tex]. Assim, pelo Lembrete 1, concluímos que os triângulos [tex]ADB[/tex] e [tex]BDC[/tex] são semelhantes.
Em ambos os triângulos, o lado proporcional à medida [tex]6[/tex] está oposto ao vértice [tex]D[/tex]. Assim, podemos afirmar que [tex]A\hat{D}B=B\hat{D}C[/tex]. Portanto, no quadrilátero [tex]ABCD[/tex], a diagonal [tex]\overline{DB}[/tex] é bissetriz do ângulo de vértice em [tex]D[/tex].
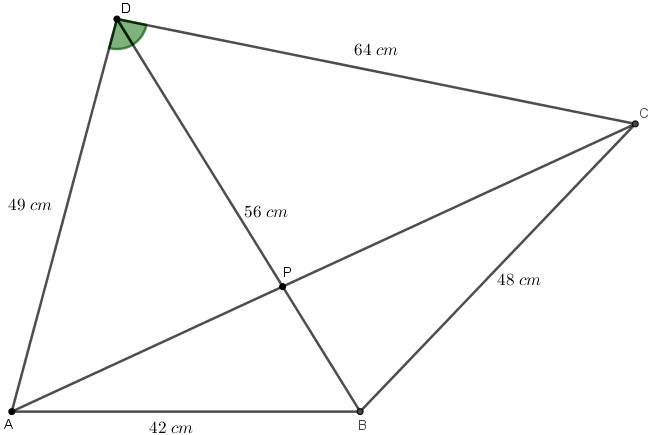
Por fim, analisando o triângulo [tex]ADC[/tex], temos que [tex]\overline{DP}[/tex] é uma bissetriz interna.
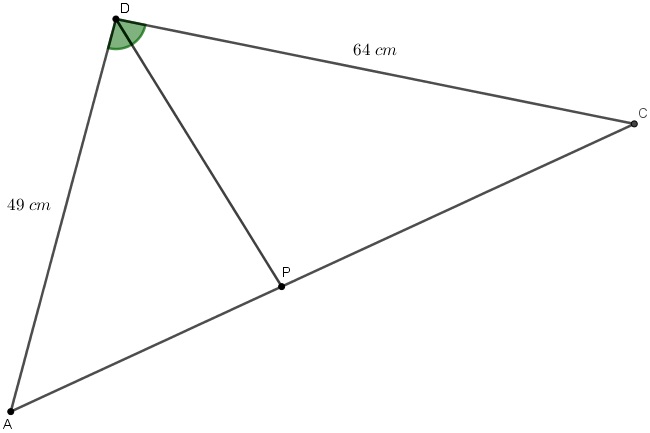
Assim, pelo Lembrete 2, segue que [tex]\dfrac{AD}{DC}=\dfrac{AP}{PC}[/tex] e, portanto, [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{AP}{PC}=\dfrac{49}{64}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
