Problema
(Indicado a partir do 9º ano do E. F.)
Um polígono convexo com [tex]k[/tex] lados de mesma medida está inteiramente contido no interior de um círculo.
Cada lado é prolongado em ambos os sentidos, até a interseção com o círculo, formando dois novos segmentos de reta fora do polígono.
Prove que é possível pintar alguns desses novos [tex]2k[/tex] segmentos de azul e o restante de vermelho, de modo que a soma dos comprimentos dos segmentos azuis seja igual à soma dos comprimentos dos segmentos vermelhos.
Uma figura para ajudar
A figura abaixo ilustra um polígono com [tex]k=5[/tex], o círculo e os segmentos previstos no enunciado do problema.
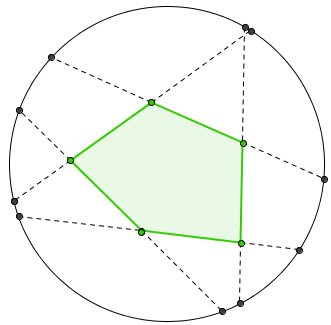
Observe que o polígono não precisa ser regular, mas deve ter todos os lados de mesma medida, isto é, deve ser equilátero.
Um resultado que ajuda
Teorema das cordas (Potência de ponto): Se duas cordas de uma mesma circunferência se intersectam, então o produto das medidas das duas partes de uma é igual ao produto das medidas das duas partes da outra.
|
|
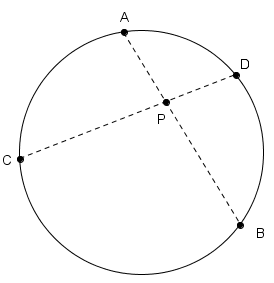
[tex]\boxed{AP \cdot PB=CP \cdot PD}[/tex] |
Solução
Considere um polígono regular com [tex]k[/tex] lados e seja [tex]x[/tex] a medida de cada lado.
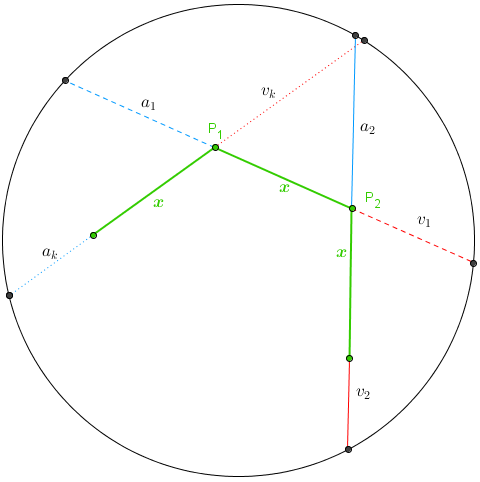
Aplicando o teorema das cordas para cada vértice [tex]P_i[/tex], com [tex]1 \leqslant i \leqslant k[/tex], e considerando que os segmentos à esquerda e à direita do lado que contém [tex]P_i[/tex] têm comprimentos [tex]a_i[/tex] e [tex]v_i[/tex], respectivamente, obtemos:
[tex]\qquad \qquad \begin{align*}
a_1(x + v_1) &= v_k(a_k + x);\\
a_2(x + v_2) &= v_1(a_1 + x);\\
a_3(x + v_3) &= v_2(a_2 + x);\\
\vdots\\
a_k(x + v_k) &= v_{k-1}(a_{k-1} + x).
\end{align*}[/tex]
Somando essas [tex]k[/tex] equações e cancelando os termos iguais, obtemos que:
[tex]\qquad \qquad \boxed{a_1 + a_2+\dots+ a_k = v_1 + v_2 +\dots + v_k}[/tex] .
Solução elaborada pelos Moderadores do Blog.